Модели массвого обслуживания

т. е. математическое ожидание продолжительности пребывания в очереди, ассоциированное с полным ансамблем требований, представляет собой сумму подансамблей требований, каждое из которых обладает приоритетом k (k — 1, 2, . . ., r).

В некоторых задачах продолжительность процедуры обслуживания завис

ит от номера (или, как говорят, от уровня) приоритета. Тогда, обеспечивая требованиям с более высокими уровнями приоритета ускоренное обслуживание, мы тем самым сокращаем среднее время ожидания в очереди, вычисленное по суммарному выходному потоку обслуженных требований. В качестве иллюстрации этого утверждения вновь обратимся к случаю, когда λ= 18, μ= 20 (так что коэффициент загруженности обслуживающей системы при этом равняется 0,9, а среднее время ожидания в очереди 0,45). Перейдем теперь к схеме обслуживания с двумя уровнями приоритета и предположим, что λ1= λ2= 9, a μ1= 30 и μ2= 15, так что коэффициент загруженности ϭ r= 9/30+9/15 = 0,9 (т. е. остается таким же, как и в схеме обслуживания при отсутствии приоритетов). С помощью (35) и (36) легко убедиться, что в этом случае средняя продолжительность пребывания в очереди требования с приоритетом 1 равняется 1/14 = 0,0714, а требования с приоритетом 2 — 10/14 = = 0,7142, т. е. меньше, чем в случае, когда μ1= μ2= μ3 = 20. При этом средняя продолжительность пребывания в очереди, вычисленная на суммарном ансамбле обслуженных требований, равняется 0,3928, т. е. оказывается меньшей по сравнению с аналогичной операционной характеристикой системы без приоритетов, а также по сравнению со случаем, когда μ1= μ2 =20.

5 Многоканальная модель с пуассоновским входным потоком и экспоненциальным распределением длительностей обслуживания

Каждому ясно, что в подавляющем большинстве случаев системы массового обслуживания являются многоканальными, и, следовательно, модели с S обслуживающими приборами (где S > 1) представляют несомненный интерес. Постулируемая при этом дисциплина очереди выглядит несколько упрощенной для большинства ситуаций, с которыми приходится сталкиваться в действительности. Тем не менее полученные здесь результаты можно рассматривать как весьма полезные, поскольку они по крайней мере позволяют в самом первом приближении оценить функциональные характеристики более сложных систем массового обслуживания.

причем длительности обслуживания взаимонезависимы как для отдельно взятого прибора, так и по системе в целом. Уравнения в конечных разностях, аналогичные приведенным в предыдущем разделе уравнениям (7) и (8) для случая одноканалъной системы массового обслуживания и определяющие значения Рп в условиях установившегося режима, имеют следующий вид:

Решение системы уравнений (3) имеет вид

Установившийся режим функционирования системы массового обслуживания, характеризующийся соотношениями (4) и (5), возможен при условии λ< μS (или < S.

В случае неограниченного количества обслуживающих приборов (например, в условиях самообслуживания) первая из формул (4) становится применимой для любого значения п. Следовательно, в этом случае Рп принимает пуассоновский вид, причем Е [п] = р.

Для такой модели используют символическое обозначение М/М/∞. При S = ∞ пуассоновский характер Рп имеет место фактически при любом виде распределения длительностей обслуживания, т. е. и в случае M/G/∞.

Формулы (4) применимы и в том случае, когда действует ограничение на суммарное количество требований М (≥S), которое может находиться в системе. При этом п ≤ М, а Р0 определяется из условия

Отметим, кроме того, что формулы (4) остаются при этом справедливыми и в случае, когда λ< μS

Операционные характеристики. Когда Рп найдены, большинство операционных характеристик рассматриваемой нами модели вычисляются с помощью элементарных алгебраических операций. К числу весьма важных характеристик системы массового обслуживания относится вероятность того, что все приборы окажутся занятыми:

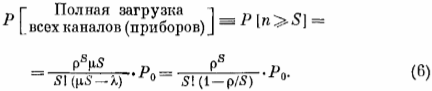
Некоторые авторы называют величину, определяемую формулой (6), вероятностью задержки; на наш взгляд, более удачным является термин виртуальная задержка. Величина определяет долю времени, в течение которого требования фактически пребывают в системе.

Введем в рассмотрение следующие величины:

В правой части (13) первое слагаемое представляет собой Е [Продолжительность ожидания в очереди], а второе — Е [Продолжительность процедуры обслуживания].

Важной особенностью данной системы является то, что ее выходной поток на интервале Т имеет пуассоновское распределение со средним значением λT обслуженных требований за единицу времени.

Рассмотрим теперь крупномасштабную систему массового обслуживания, состоящую из групп последовательно включенных приборов, т, е. организованных таким образом, что выходной поток одной группы приборов оказывается входным для другой группы приборов.

Если каждую из подобных групп приборов можно описать с помощью многоканальной модели рассмотренного выше типа, то средние значения операционных характеристик системы легко вычислить, проанализировав вначале каждую из групп как совершенно автономную, а затем сложив полученные результаты в предположении, что частоты поступления требований λ, на входе каждой из групп одинаковы.

6 Процессы рождения и гибели

В данном разделе дается унифицированное описание аналитических процедур, которые были нами использованы при рассмотрении процессов частного вида, и одновременно демонстрируется способ построения модели, которая помогает также анализировать ситуации несколько иного характера. Описываемые этой моделью процессы называются процессами рождения и гибели.

Для начала будем предполагать, что вероятности переходов с течением времени не меняются, т. е. будем постулировать, что рассматриваемый нами процесс является однородным во времени.

Будем считать, что исследуемая система функционирует непрерывно, т. е. не имеет определенной стартовой точки, и в момент t характеризуется количеством находящихся в ней требований, которое мы обозначим через п (п = 0, 1, 2, . . .). Нам, разумеется, нужно договориться относительно выбора на оси времени начала отсчета t. Пусть в качестве начала отсчета времени выбрана точка t = 0; обозначим одновременно через i количество требований, находящихся в системе в момент 0. Пусть, по определению,

 Скачать реферат