Модели массвого обслуживания

Об анализе систем массового обслуживания. Проведенное до этого краткое обсуждение различных типов систем массового обслуживания носило явно фрагментарный характер.

Но и его достаточно, чтобы представить, насколько многообразно и многочисленно семейство таких систем и соответствующих им математических моделей. Каждый из возможных вариантов нетрудно описать на строгом математическом языке; од

нако это часто почти ничего не дает, если оценивать результаты, получаемые на основе такого рода описаний, с практической точки зрения. Поэтому при анализе систем массового обслуживания в большинстве случаев практикуется комбинированное применение следующих двух подходов к решению такого рода задач.

Первый подход заключается в использовании для приближенных описаний реальной системы простых математических моделей, наподобие тех, что приводятся в данной главе. Затем, располагая результатами анализа исходных простых моделей и используя эти результаты в качестве некоторого ориентира, операционист может разработать имитационную модель, которая с помощью ЭВМ позволит учесть те аспекты задачи, которые, являясь существенными, в то же время трудно поддаются анализу на первом этапе математического моделирования.

Ответ на вопрос о том, какие операционные характеристики являются наиболее важными для формирования управляющих решений, разумеется, может быть дан лишь с учетом конкретных условий задачи. Однако следует отметить, что операциониста, как правило, интересуют распределения вероятностей для числа поступивших в систему требований и для длительностей их ожидания или по крайней мере средние значения случайных переменных, описывающих эти характеристики, на большом отрезке времени. Кроме того, иногда требуется знать вероятность того, что все обслуживающие приборы окажутся свободными или занятыми; распределение вероятностей для продолжительности свободных или, наоборот, занятых периодов; вероятность того, что длина очереди (число ожидающих требований) превысит некоторое наперед заданное число, а также распределение вероятностей для интервала между последовательными моментами завершения процедур обслуживания. Если модель массового обслуживания не очень сложна, то для всех упомянутых выше характеристик удается получить строгие, записанные в явном виде аналитические выражения, весьма удобные для вычислений; именно так обстоит дело в настоящей главе. Однако по мере усложнения условий задачи эти показатели нередко удается выразить лишь в виде неявных функций фигурирующих в задаче переменных т. е. представить с помощью так называемых трансформ.

2 Распределение вероятностей для длительности интервалов между последовательными поступлениями требований на обслуживание

Механизм поступления требований удобнее всего описывать, задавая распределение вероятностей для длительностей интервалов времени между последовательными поступлениями требований на обслуживание. Предположим, что продолжительности интервалов между поступлениями требований статистически независимы, определяются одним и тем же распределением вероятностей и описываются некоторой непрерывной функцией, представляющей собой плотность распределения. Такого рода входной поток требований представляет собой типичный пример так называемого процесса восстановления, а последовательность поступлений является иллюстрацией так называемой последовательности рекуррентных событий. Пусть f(t) есть плотность распределения продолжительностей (t) интервалов между любой парой смежных поступлений (при этом t≥0). Определим также величину 1/λ как среднее значение длительности временного интервала между поступлениями требований, так что λ можно интерпретировать как среднее число поступлений в единицу времени, или как среднюю частоту поступлений. Если функция f(t) задана, значение λ выражается через математическое ожидание

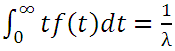
(средняя длительность интервала между поступлениями) (1)

Так, например, если единицей времени является 1 ч, а λ = 4 есть среднее количество поступлений в течение часа, то 1/λ = 0,25 ч, т. е. в среднем в течение каждой четверти часа в систему поступает одно дополнительное требование. Аналогично, если каждые 10 мин в систему поступает в среднем одно требование, то частота поступления λ равняется 0,1 требование/мин.

Случайные поступления. Наиболее важный пример распределения длительностей интервалов между поступлениями требований соответствует случаю совершенно случайных поступлений. Термин «совершенно случайный» означает, что вероятность поступления требования в любом достаточно малом интервале (Т, Т + К) зависит только от длины интервала h и не зависит ни от положения на оси времени «стартовой» точки Т, ни от протекания процесса поступлений требований на обслуживание в моменты времени, предшествующие Т. Другими словами, входной поток является стационарным (или, как его нередко называют, однородным) и не обладает памятью. Ниже мы дадим строгое доказательство того, что предположение о совершенно случайном характере поступлений эквивалентно записи

f(t)=, t≥0 (2)

(экспоненциальное распределение со средним значением 1/λ и дисперсией 1/λ2),

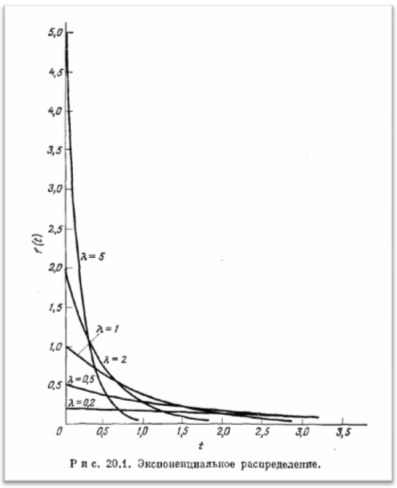
где е — основание натурального логарифма (е = 2,71818 . . .).

Ряд графиков экспоненциального распределения, соответствующих различным значениям λ приведен на рисунке.

Для проверки того, что экспоненциальное распределение не обладает памятью, допустим, что стартовой точкой является точка

t = 0. Тогда вероятность отсутствия поступлений на интервале (0, Т) равняется вероятности того, что первое поступление имеет место после момента времени Т:

Р[t≥T]= =(3)

При этом условная вероятность отсутствия поступлений на интервале (0, Т + К) при условии, что не было ни одного поступления

на интервале (0, Т), по определению равняется

= == P[t≥h] (4)

т.е. зависит только от h. Согласно (4), вероятность отсутствия поступлений на интервале

(T, Т +h) остается одной и той же независимо от того, отсутствуют ли поступления на интервале (0, Т) или в момент времени Т имеет место поступление требования и, следовательно, наблюдается акт возобновления потока.

Существует другой способ доказательства того, что события, фигурирующие в экспоненциальных процессах, носят совершенно случайный характер. Здесь идея доказательства излагается грубо приближено, но это доказательство можно сделать и абсолютно строгим. Пусть на интервале (0, Т) количество поступлений равняется п. Тогда, если длительности интервалов между последовательными поступлениями распределены по экспоненциальному закону, моменты поступлений распределены на интервале (0, Т) взаимонезависимо и равномерно. Эти соображения можно положить в основу целого ряда статистических испытаний, позволяющих установить, насколько адекватно экспоненциальное распределение описывает реальные процессы формирования очереди на входе системы массового обслуживания. Свойства экспоненциального распределения длительностей интервалов между последовательными поступлениями становятся более прозрачными, если воспользоваться разложением в ряд Тейлора

 Скачать реферат