Теория статистики

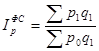
Взаимосвязь индексов этой группы

Тема: Изучение взаимосвязи социально-экономических явлений

Социально-экономические явления представляют собой результат воздействия большого числа причин (факторов)

Признаки делят на:

факторные

результативные

Связь м/у факторными и результативными признаками может быть:

функциональной, при которой каждому значению факторного признака соответствует одно значение результативного признака

стохастической, когда причинная зависимость проявляется не в каждом отдельном случае, а в общем среднем при большом числе наблюдений. Частным случаем является корреляционная связь при которой изменение среднего значения результативного признака обусловлено изменением факторных признаков.

Связи м/у явлениями и их признаками классифицируются по степени тесноты, направлению и аналитическому выражению

По степени тесноты различают количественные оценки тесноты связи

По направлению связь бывает:

прямая (+)

обратная (-)

По аналитическому выражению:

Прямолинейная (линейная)

Нелинейная (криволинейная)

- парабола

- гипербола

Для выявления количества связей, ее характера и направления в статистике используют следующие методы:

1. Метод приведения параллельных данных

2. метод аналитических группировок

3. Графический метод

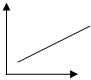
4. Метод корреляции

Корреляция – статистическая зависимость м/у случайными величинами не имеющая строгофункционального характера, при котором изменение одного из случайных величин приводит к изменению математического ожидания другой.

В статистике различают следующие варианты зависимости:

Ø Парная корреляция – связь м/у двумя признаками (результативным и факторным, или двумя факторными)

Ø Частная корреляция – зависимость м/у результативным и одним факторным признаком, при фиксированном значении других факторных признаков

Ø Множественная корреляция зависимость результативного и 2-х и более факторных признаков включенных в исследование

Корреляционный анализ имеет задачи:

1. отыскание математической формулы, которая выражала бы зависимость y от x

2. измерение тесноты такой зависимости

Решение 1 задачи осуществляется в регрессионном анализе и нахождении уравнения регрессии (уравнение связи)

Параметры для всех уравнений связи определяют из системы нормальных уравнений, отвечающих требованию метода наименьших квадратов

Система нормальных уравнений при линейной зависимости

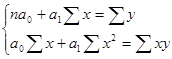
а0 – параметр, выражающий суммарное влияние всех неучтенных факторов

а1 – коэффициент выражающий усредненное влияние фактора х на результат у

Если связь выражена параболой второго порядка , то система нормальных уравнений для отыскания параметров а0, а1 и а2 выражается следующим образом

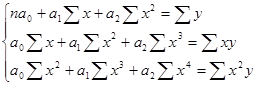
Измерение тесноты связи для всех форм связи может быть решена с помощью исчисления теоретического корреляционного отношения (ŋ)

Где

- факторная дисперсия

- дисперсия фактического значения признака

d - средний квадрат отклонений расчетных значений результативного признака от средней фактической результативного признака. Т.к. d2 отражает вариацию в ряду только за счет вариации фактора х, а дисперсия s2 отражает вариацию у за счет факторов то их отношение, именуемое теоретическим коэффициентом детерминации, показывает какой удельный вес в общей дисперсии ряда у занимает дисперсия, вызываемая вариацией фактора х. Квадратный корень из отношения этих дисперсий дает нам теоретическое корреляционное отношение.

Если d2=s2 то это означает, что роль других факторов в вариации сведена на нет. И отношение , означает полную зависимость вариации у от х.

Если d2=0, значит вариация х никак не влияет на вариацию у и ŋ=0

Т.о. корреляционное отношение может быть от 0 до 1.

В случае линейной зависимости

- линейный коэффициент корреляции

В случае небольшого числа наблюдений n очень важно оценить надежность (значимость) коэффициента корреляции. Для этого определяют среднюю ошибку коэффициента корреляции по следующей формуле:

Где n-2 – число степеней свободы при линейной зависимости, затем находят отношение коэффициента корреляции к его средней ошибке

, которое сравнивается с табличным значением t-критерия Стьюдента. Если t фактического (расчетное) больше t табличного, то линейный коэффициент корреляции r считается значимым, а связь м/у х и у реальной.

 Скачать реферат