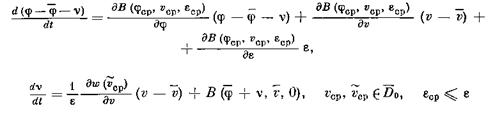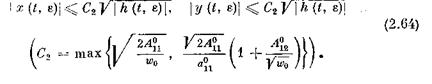Асимптотика решений дифференциальных уравнений
и поэтому она единственным образом разрешима относительно этих функций. По правилу Крамера имеем:
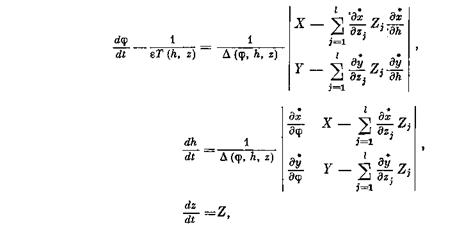
или, в силу свойств 7, 6, 5:
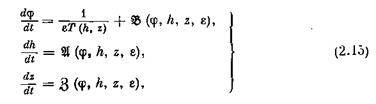
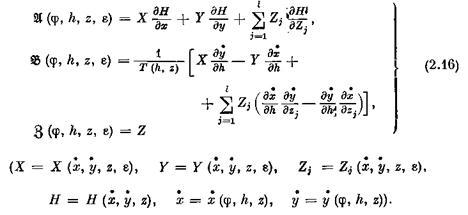
Пусть при
![]()
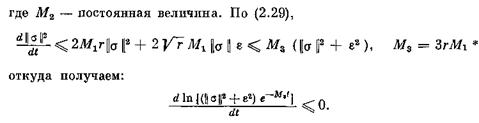
Из последнего соотношения следует:
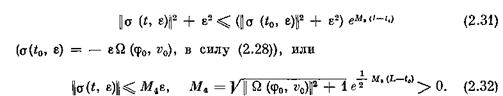
![]()
![]()
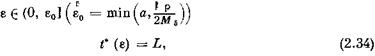
Так как в противном случае
что противоречит определению
![]()
Оценим
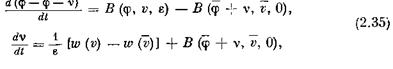
В силу (2.19), (2.20) и (2.22),
или, по формуле конечных приращений,
|
|
(применимость формулы конечных приращений следует из (2.24)). Следовательно, в силу ограниченности функций w (v), В (φ, v, е) и всех их частных производных в области значений, по (2.33), (2.34) имеем:
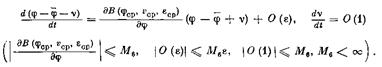
Поэтому
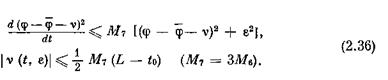
Из (2.36) следует:
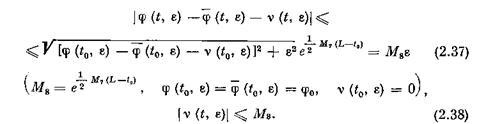
Соотношения (2.33), (2.34), (2.37), (2.38) полностью доказывают теорему об усреднении (м° = max (М5, Мв), е0 = min(a,^)).
Вернемся к доказательству теоремы 1. Так как система (2.15) типа (2.19), то, по теореме об усреднении, существует число е0 > 0 такое, что при любых eg (0, е0], t 6 [*<>> L] решение {ф (t, е), h (t, е), z (t, г)} системы (2.15) с начальными условиями
![]()
и решение {ф (t, e), h(t), z (t)} усредненной системы (2.17) с теми же начальными условиями
![]()
связаны следующим образом: точка {h (t, e), z (t, г)} остается в некоторой и выполняются соотношения:
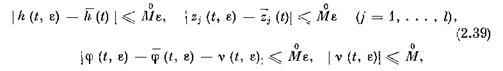
![]()
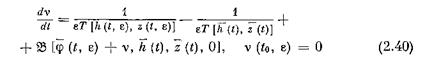
окрестность решения)). А так как, по (2.13),
![]()
![]()
и так как точка {h (£, е), z (t, е)} остается в Ghp CZ Gh, то на отрезке [tQ, L] при любом 8 g (0, е0] решение {х (t, е),?/ (£, е), z (£, г)} системы (2.1) остается в G, причем, по свойству 3,
В силу же (2.13),
![]()
и потому соотношения (2.39), (2.40) доказывают первую часть теоремы 1. Докажем вторую часть теоремы 1. По формуле конечных приращений, из (2.41) получаем:
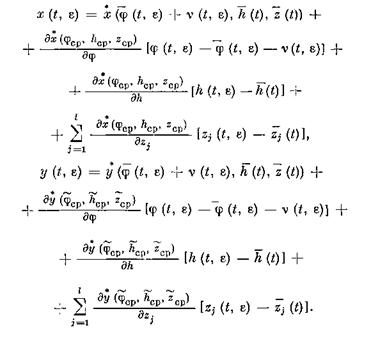
Возникает вопрос, как ведут себя решения системы (2.1) во всей указанной окрестности Go (включая и положения равновесия {/ (z), g (z), z} системы (2.3)). На этот вопрос отвечают теорема 1 и нижеследующие теоремы 2 и 3.
ТЕОРЕМА 2. Пусть в окрестности Go выполнены условия теоремы 1, касающиеся гладкости правых частей системы (2.1). Тогда найдется число 8° у> О, такое, что при любом г £ (0, е°] (е° <^ а) на конечном промежутке времени [to,L] решение {х (t, е), у (t, е), z (t, г)} системы (2.1) с начальными условиями вырожденной системы
![]()
![]()
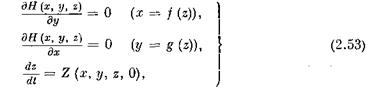
остается в Go и с точностью до величин порядка О (г) совпадает с решением
проходящим при t — to через то же положение равновесия
(предполагается, что решение {х (t), у (t), z (t)} остается в G на [t0, L]). Доказательство. Не нарушая общности рассуждений, будем считать, что в Go
![]()
1 1 так как замена переменных х, у, zx, ., zt на х, у, z1? z> и Н
на Я1, где
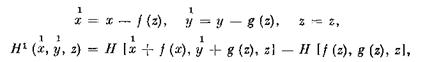
![]()
сохраняет вид системы (2.1), но дает условия (2.54). Следовательно, в силу.
Это решение на конечном промежутке времени [t0, L] составляет некоторое замкнутое ограниченное множество FQ CZ G0 и поэтому найдется ро > 0 такое, что G00 С G0 (GQ0 — р0-окрестность F0).
|
|
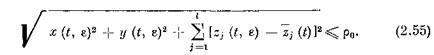
Положим
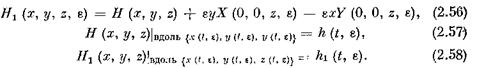
В силу (2.56) и (2.1), вдоль решения {х (£, е), у (t, е), z (t, &)} имеем:
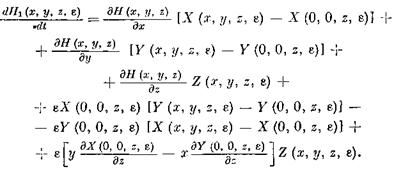
Следовательно, по формуле Тейлора, примененной к функциям
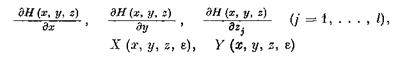
относительно х, у в G00, в силу (2.54), (2.58), получим на [t0, t^ (г)]:
![]()
(формула Тейлора применима в G00 относительно х, у, так как прямолинейный отрезок, соединяющий любые две точки (я, у, z) и (0, 0, z) из Goo, содержится в Goo, поскольку каждое сечение области G00 плоскостью z = const представляет собой круг с центром в точке (0, 0, z), по определению Goo).
Функция О2 (х, у, е), в силу указанной в условиях теоремы гладкости правых частей системы (2.1), является однородной квадратичной относительно х, у, е с ограниченными в Goo коэффициентами, и поэтому
![]()
![]()
постоянная величина).
С другой стороны, по формуле Тейлора, в силу (2.54) имеем в G00
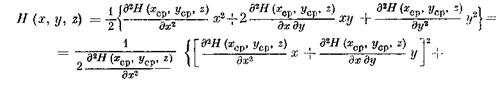
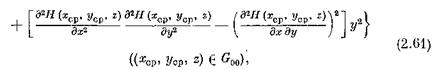
и так как при (х, у, z)
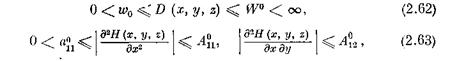
то соотношение (2.61), в силу (2.57), дает на [£0, t(е)]:
|
|
Другие рефераты на тему «Математика»:
Поиск рефератов
Последние рефераты раздела
- Анализ надёжности и резервирование технической системы
- Алгоритм решения Диофантовых уравнений
- Алгебраическое доказательство теоремы Пифагора
- Алгоритм муравья
- Векторная алгебра и аналитическая геометрия
- Зарождение и создание теории действительного числа
- Вероятностные процессы и математическая статистика в автоматизированных системах