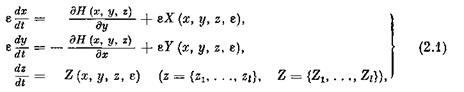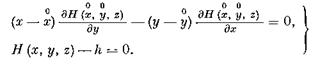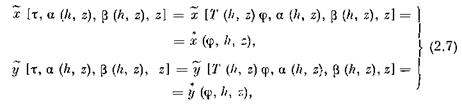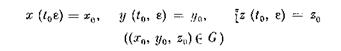Асимптотика решений дифференциальных уравнений
Асимптотические формулы для решения этой системы находятся для области, где траектории соответствующей гамильтоновой системы «быстрых движений» при каждом векторе z замкнуты (в случае невырожденного центра в рассматриваемую область включается и сам центр). Метод исследования системы (1.3) таков: сначала рассматривается система «быстрых движений» (1.4), а затем система (1.3) после соответствующе
й замены переменных усредняется вдоль решений (1.4). Оказывается, что уравнение с малым параметром и. при старшей производной и с пропущенной в основном члене Q (п — 1)-й производной, исследованное В.М. Волосовым (при п — 2 — в работе (12Г), при F ~ О — в 'работах (8) — (п)) методом конечных разностей, является частным случаем системы (1.3). Поэтому результаты работ (8) — (12) (эти результаты сформулированы в § 3 настоящей работы) следуют из результатов § 2.
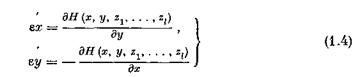
Метод построения решения уравнения (1.5) при п = 2 с любой наперед заданной точностью в случае, когда известно общее решение (в форме разложения в тригонометрический ряд Фурье) соответствующего невозмущенного уравнения был дан в работе Ю.А. Митрополъским.
![]()
Задача исследования системы (1.3) с точки зрения работ (3) — (4) и вывода из нее известных результатов В.М. Волосова [работы (8) — (12)] относительно уравнения (1.5) была поставлена Л.С. Понтрягиным в его докладе на семинаре В.И. Смирнова в Ленинграде в середине апреля 1957 г.
Выражаю глубокую благодарность Л.С. Понтрягину за ценные указания, советы и постоянное внимание к настоящей работе.
1.1 Асимптотическое поведение решений системы
Система (1.3) в векторной форме имеет вид:
|
|
|
|
глк, в быстром времени
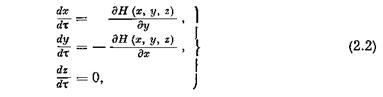
При е = 0 система (2.1') переходит в гамильтонову систему
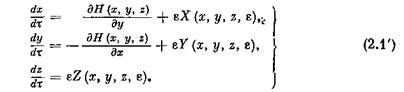
являющуюся системой «быстрых движений» для системы (2.1). 1. Изучение системы (2.2). Пусть функции
![]()
определены и непрерывны вместе со всеми своими первыми частными производными в некоторой области G эвклидова пространства E2+i переменных х, у, zi, ., zi. Как известно, система (2.2) имеет первый интеграл
![]()
и (2.3) представляет собой семейство всех фазовых траекторий системы(2.2) на кажтгой плоскости z = const области G.
Возьмем некоторую точку (х, у, z) из G, не являющуюся положением равновесия системы (2.2). По известной теореме существования и единственности решений системы обыкновенных дифференциальных уравнений, через эту точку пройдет только одна фазовая траектория системы
(2.2). Уравнение этой траектории запишется в виде:
![]()
(см. (2.3)).
Докажем следующее утверждение.
Пусть траектория (2.4) замкнута и целиком лежит внутри области G. Тогда в пространстве E2+i существует некоторая окрестность G этой траектории (2.4) такая, что
1) фазовые траектории системы (2.2), проходящие через точки G, замкнуты и целиком лежат в G;
2) уравнение (2.3) при каждой паре (/г, z) определяет одну и только одну фазовую траекторию системы (2.2), расположенную в G;
3) на каждой фазовой траектории (2.3) системы (2.2), лежащей в G, можно выбрать по одной точке ![]() , гладко зависящей от
, гладко зависящей от
![]()
В самом деле, в силу известных свойств гамильтоновой системы, в пространстве E2+i существует некоторая окрестность G траектории (2.4) (Gd G), в которой выполняется условие 1). Выделим из G ту окрестность траектории (2.4), в которой выполняются и условия 2), 3). Для этого возьмем поверхность, пересекающую каждую плоскость z = const области G
о о по нормали в точке (х, у, z) к фазовой траектории системы (2.2), проходящей через эту точку. Уравнение этой поверхности имеет вид:
![]()
Следовательно, точка (х, у, z, h) эвклидова пространства £"2+z переменных х, у, z, h удовлетворяет системе
|
|
Левые части системы (2.5) определены и непрерывны вместе со всеми своими частными производными в области Г: (#, у, z) £ G, —ос <^ /г<^оо. Якобиан системы (2.5)
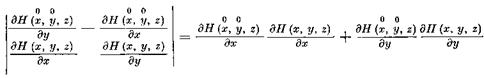
отличен от нуля в точке (х, у, z, /г), так как точка (х,?/, z) не является положением равновесия системы (2.2). Поэтому, по теореме о неявных функциях, в некоторой окрестности Г° точки (х, у, z, h) (Г°С Г) система (2.5) разрешима относительно х и у:
![]()
причем
![]()
являются однозначными функциями от /г, zi, ., zx, непрерывными по совокупности этих переменных вместе со всеми своими первыми частными производными. Следовательно, целые фазовые траектории системы (2.2), проходящие через точки
![]()
составляют искомую окрестность G траектории (2.4). Пусть
![]()
— решение системы (2.2) с начальными условиями
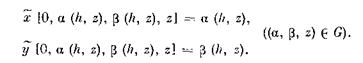
![]()
Решение (2.6) системы (2.2) является периодическим, поскольку описывает замкнутую траекторию (2.3). Тогда, полагая получим:
|
|
2. Изучение системы (2.1). Исследуем решение
![]()
системы (2.1) с начальными условиями
|
|
на конечном промежутке времени Uo, L]. Имеет место
Другие рефераты на тему «Математика»:
Поиск рефератов
Последние рефераты раздела
- Анализ надёжности и резервирование технической системы
- Алгоритм решения Диофантовых уравнений
- Алгебраическое доказательство теоремы Пифагора
- Алгоритм муравья
- Векторная алгебра и аналитическая геометрия
- Зарождение и создание теории действительного числа
- Вероятностные процессы и математическая статистика в автоматизированных системах