Аффинные преобразования евклидовой плоскости в сопряжённых комплексных координатах

3) (ортогональное сжатие).

Тогда , где . Найдём формулу преобразования f.

1. Сначала найдём формулу преобразования : height=41 src="images/referats/3153/image189.png">.

2. Найдём формулу для преобразования f: , откуда получаем - это формула эллиптического поворота.

Проверим, будет ли определитель рассматриваемого преобразования не равен нулю. Преобразуем выражение определителя

, используя равенство , тогда получим, что . Следовательно, определитель преобразования не равен нулю, и f является аффинным преобразованием, что и требовалось доказать.

Так как определитель рассматриваемого аффинного преобразования положителен, то эллиптический поворот – это аффинное преобразование первого рода.

Это преобразование имеет единственную неподвижную точку О, значит оно является центроаффинным. При этом преобразовании каждая точка М плоскости (М≠О) переходит в другую точку, которая принадлежит соответствующему эллипсу. Этот эллипс при рассмотренном преобразовании переходит сам в себя. Преобразование с объявленными свойствами называется эллиптическим поворотом.

Выясним, имеет ли эллиптический поворот инвариантные пучки параллельных прямых. Для этого найдём дискриминант характеристического уравнения этого преобразования. Комплексные координаты векторов при аффинном преобразовании (2) переходят в коллинеарные им векторы по формуле , откуда получаем уравнение . Решая его, получим характеристическое уравнение . Найдём (), его значение равно , тогда характеристическое уравнение запишется в виде: . Его дискриминант отрицателен (так как ). Следовательно, f – аффинное преобразование с единственной неподвижной точкой О и не имеющее инвариантных пучков параллельных прямых, то есть эллиптический поворот – эквицентроаффинное преобразование.

Формулу (29) эллиптического поворота можно записать в виде системы условий: 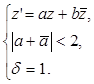Эту формулу можно представить иначе: , то есть эллиптический поворот является композицией сжатия к действительной оси и подобия первого рода с центром в точке О.

§4. Параболический поворот

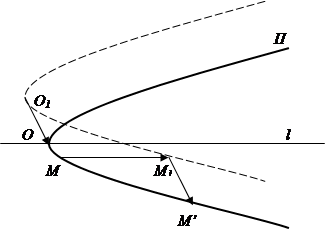
Покажем, что параболу можно перевести в себя при преобразовании её с помощью композиции сдвига и параллельного переноса, не параллельного оси сдвига. Пусть М – произвольная точка параболы П с осью l (рис. 6), примем эту ось за действительную. Произведём сдвиг с этой же осью l: , где , . Этот сдвиг переведёт точку М в точку М1 и параболу П – в параболу П1. Параболы П и П1 равны с точностью до сдвига.

Рис. 6

Теперь произведём параллельный перенос параболы П1: (), где . Тем самым, парабола П1 перейдёт в параболу П, а точка М1 перейдёт в точку М’ параболы П.

Таким образом получили, что парабола переходит в себя при преобразовании её с помощью композиции сдвига и параллельного переноса, не параллельного оси сдвига [1,3]. Это преобразование называется параболическим поворотом и имеет формулу , где , , (30)

Определитель найденного преобразования . Так как определитель отличен от нуля, параболический поворот является аффинным преобразованием, а так как он больше нуля, - аффинным преобразованием первого рода.

Найдём собственные числа параболического поворота аналогично тому, как делали это для других рассмотренных аффинных преобразований. Найдём собственные числа λ из условия . В процессе нахождения приходим к характеристическому уравнению , но так как , характеристическое уравнение примет вид , откуда . Следовательно параболический поворот имеет только один инвариантный пучок параллельных прямых, параллельных оси сдвига.

§5. Представление аффинных преобразований композициями их частных видов

Выше мы имели целый ряд примеров аффинных преобразований. Мы знаем также ряд свойств, которыми обладают все аффинные преобразования. Найдём общую конструкцию, позволяющую получить любое аффинное преобразование. Такая конструкция указывается следующей теоремой:

Любое аффинное преобразование может быть представлено в виде композиции родства и подобия.

Докажем это утверждение. Любое аффинное преобразование имеет формулу (2) вида , где . Вспомним формулы родства и подобия. Родство задаётся равенством , где , а подобие - или . Преобразуем формулу (2) аффинного преобразования следующим образом: , её можно представить как:

 Скачать реферат