Некоторые линейные операторы
U = -![]() *
*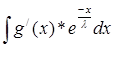
Подставим U и V в f(x) = U(x)*V(x) и получим:
f(x) = с1*![]() *(-
*(-![]() )*
)*
найдем интеграл Y = 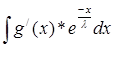 , интегрируем по частям:
, интегрируем по частям:
dz = g/(x)dx;
z = 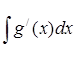 = g(x);
= g(x);
j = ![]() ;
;
dj = - ![]() *
*![]() dx;
dx;
Y = g(x)* ![]() +
+ ![]() *
*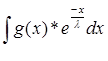
Подставим полученное значение в выражение f(x), которое примет вид:
f(x) = -![]() -
- ![]() *
*![]() *
*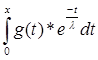 ;
;
Получим оператор В:
Bg = -![]() -
- ![]() *
*![]() *
*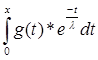 ;
;
x ![]() [0,b], t
[0,b], t ![]() [0,x], g(x)
[0,x], g(x) ![]() S,
S, ![]() - произвольное число.
- произвольное число.
Оператор В не существует, если ![]() = 0;
= 0;
Рассмотрим ограниченность оператора В для всех ![]()
![]() R,
R, ![]()
![]() 0;
0;
||Bg|| = ||f(x)|| = ![]() |f(x)| =
|f(x)| = ![]() |-
|-![]() -
- ![]() *
*![]() *
*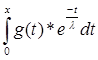 |
| ![]()
![]() (|
(|![]() | + |
| + |![]() *
*![]() *
*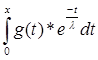 |)
|) ![]()
![]() |
|![]() | +
| + ![]() |
|![]() *
*![]() *
*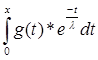 |
| ![]()
![]() |
|![]() | +
| + ![]() |
|![]() *
*![]() |*
|*![]() |g(x)*
|g(x)* ![]() |*|x|
|*|x| ![]()
![]() *
*![]() |g(x)| +
|g(x)| + ![]()
![]()
![]() *
*![]() |g(x)|*
|g(x)|* ![]() (|
(|![]() |*|x|)
|*|x|) ![]()
![]() |g(x)|*(
|g(x)|*( ![]() +
+ ![]() *
*![]()
![]() *
*![]()
![]() *b);
*b);
При ![]() > 0
> 0
![]()
![]() =
= ![]() ;
;
![]()
![]() = 1;
= 1;
При ![]() < 0
< 0
![]()
![]() =1;
=1;
![]()
![]() =
= ![]() ;
;
Эти оба случая можно записать в общем виде: ![]() {1,
{1, ![]() }, тогда
}, тогда
![]() |g(x)|*(
|g(x)|*( ![]() +
+ ![]() *
*![]()
![]() *
*![]()
![]() *b)
*b) ![]()
![]() |g(x)|*(
|g(x)|*( ![]() +
+ ![]() *
*![]() {1,
{1, ![]() }*b) = ||g(x)||*(
}*b) = ||g(x)||*( ![]() +
+ ![]() *
*![]() {1,
{1, ![]() }*b);
}*b);
Другие рефераты на тему «Математика»:
Поиск рефератов
Loading
Последние рефераты раздела
- Анализ надёжности и резервирование технической системы
- Алгоритм решения Диофантовых уравнений
- Алгебраическое доказательство теоремы Пифагора
- Алгоритм муравья
- Векторная алгебра и аналитическая геометрия
- Зарождение и создание теории действительного числа
- Вероятностные процессы и математическая статистика в автоматизированных системах
