Некоторые понятия высшей матаматики

б) <0 (гиперболический вид) A’C’<0 (разные знаки). Пусть A’>0

A`=, , , тогда .

Если F0=0, то , получаем пару пересекающихся прямых.

Если F0>0, то (гипербола)

Если F0<0, то (гипербола, где оси поменялись местами)

в) (параболический тип) A`C`=0

(5)

а) D`=E`=0, пусть

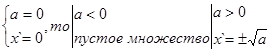
б)

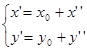
** в (5)

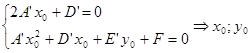
, где 2р=, если p>0, то парабола .

Теория пределов

Число а называется пределом последовательности xn для любого () сколь угодно малого положительного числа найдется номер, зависящий от , начиная с которого все члены последовательности отличаются от а меньше, чем на .

Предел последовательности

Под числовой последовательностью понимают функцию , заданную на множестве натуральных чисел т.е. функцию натурального аргумента.

Число a называется пределом последовательности xn (x=1,2,…): =а, если для любого сколь угодно малого >0, существует такое число N=N(), что для всех натуральных n>N выполняется неравенство .

1) , - натуральное число. Если xn=a, то (a, a, a, a) – стационарная последовательность.

2) , где a, d – const, тогда (a, a+d, a+2d,…a+(n-1)d)

xn+1=xn+d – рекуррентная формула.

3) Числа Фибоначчи. (1,1, 2, 3, 5, 8, 13, 21,…), где x1, x2 =1 и .

(*);

- эпсилон – окрестность числа а.

1. .

2.

Основные теоремы пределах

1. О единственном пределе. Последовательность имеет не более 1 предела.

2. Предельный переход в неравенстве.

3. О трех последовательностях. О сжатой последовательности.

 Скачать реферат