Теория остатков

Случай 2. Пусть теперь c 0. Этот случай закрывается следующей теоремой.

Теорема. Пусть ( a , b ) = 1, { x 0 , y 0 } - частное решение диофантова уравнения ax + by = c . Тогда его общее решение задается формулами:

Таким образом, и в теории линейных диофантовых уравнений общее решение неоднородного уравнения есть сумма общего решения соответствующего однородного уравнения и некоторого (любого) частного решения неоднородного уравнения.

Доказательство. То, что правые части указанных в формулировке теоремы равенств действительно являются решениями, проверяется их непосредственной подстановкой в исходное уравнение. Покажем, что любое решение уравнения ax + by = c имеет именно такой вид, какой указан в формулировке теоремы. Пусть { x * , y *} - какое-нибудь решение уравнения ax + by = c . Тогда ax * + by * = c , но ведь и ax 0 + by 0 = c . Следуя многолетней традиции доказательства подобных теорем, вычтем из первого равенства второе и получим:

a ( x *- x 0 ) + b ( y *- y 0 ) = 0

- однородное уравнение. Далее, глядя на случай 1, рассмотрение которого завершилось несколькими строками выше, пишем сразу общее решение: x *- x 0 = - bt , y *- y 0 = at , откуда моментально, используя навыки третьего класса средней школы, получаем:



Как же искать то самое частное решение { x 0 , y 0 }. Мы договорились, что ( a , b ) = 1. Это означает, что найдутся такие u и v из Z , что au + bv = 1, причем эти u и v мы легко умеем находить с помощью алгоритма Евклида. Умножим теперь равенство au + bv = 1 на c и получим: a ( uc ) + b ( vc ) = c , т.е. x 0 = uc , y 0 = vc .

Определение. Цепной (или, непрерывной) дробью называется выражение вида:

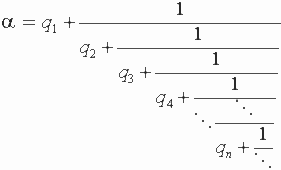
(Бедные наборщики в докомпьютерные времена буквально стрелялись, когда им приходилось набирать в книжках подобные многоэтажные выражения.) Договоримся называть числа q 1 , q 2 , ., q n , . - неполными частными и считаем, что q 1 Z , а q 2 , ., q n , . N . Числа называются подходящими дробями цепной дроби .

Цепная дробь может быть как конечной (содержащей конечное число дробных линий и неполных частных), так и бесконечной вниз и вправо (на юго-восток). В первом случае она, очевидно, представляет некоторое рациональное число, во втором случае - пока непонятно что она вообще из себя представляет, но ясно, что все ее подходящие дроби - рациональные числа.

Пусть Q , = a / b ; a , b Z , b > 0. Оказывается, что при этих условиях, указанный выше процесс разложения числа в цепную дробь всегда конечен и выполним с помощью достопочтенного и любимого нами алгоритма Евклида. Действительно, отдадим алгоритму числа a и b , и внимательно посмотрим, что получится.

Значит:

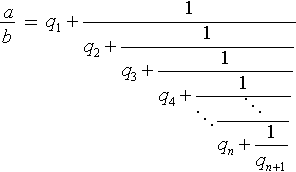
где q 1 , q 2 , ., q n +1 - как раз те самые неполные частные из алгоритма Евклида (вот откуда название этих чисел в цепных дробях). Таким образом, в случае рационального числа a / b , процесс разложения в цепную дробь конечен и дробь содержит не более b этажей. Наиболее одаренные читатели в этом месте уже поняли, что основная теорема о цепных дробях для рациональных чисел оказалась почти доказана (не доказали только единственность разложения, но она в случае конечных цепных дробей почти очевидна - приравняйте две цепных дроби и, рассуждая по индукции, получите, что у равных дробей совпадают все неполные частные).

Пример. Пример заимствован из книги И. М. Виноградова "Основы теории чисел". Итак: разложить 105/38 в цепную дробь.

Включаем алгоритм Евклида:

105 = 38 · 2 + 29

38 = 29 · 1 + 9

29 = 9 · 3 + 2

9 = 2 · 4 + 1

2 = 1 · 2

Неполные частные я специально подчеркнул потому, что теперь для написания ответа нужно аккуратно расположить их подряд на этажах цепной дроби перед знаками плюс:

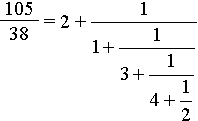
2 Делимость в кольцах

2.1 Область целостности

Область целостности (или целостное кольцо, или область цельности) — понятие абстрактной алгебры: ассоциативное коммутативное кольцо с единицей, в котором 0≠1 и произведение двух ненулевых элементов не равно нулю. Условие 0≠1 исключает из рассмотрения тривиальное кольцо {0}.

Эквивалентное определение: область целостности — это ассоциативное коммутативное кольцо, в котором нулевой идеал {0} является простым. Любая область целостности является подкольцом своего поля частных.

Примеры

· Простейший пример области целостности — кольцо целых чисел .

· Любое поле является областью целостности. С другой стороны, любая артинова область целостности есть поле. В частности, все конечные области целостности суть конечные поля.

· Кольцо многочленов с коэффициентами из некоторого целостного кольца также является целостным. Например, целостными будут кольцо многочленов одной переменной с целочисленными коэффициентами и кольцо многочленов двух переменных с вещественными коэффициентами.

 Скачать реферат