Разработка методики обучения интегрального исчисления функции двух переменных

2. Пусть поле осуществляет преобразование области в область , имеет кусочно–гладкую границу.

3. Пусть области 1 src="images/referats/27477/image207.png">и являются ограниченными.

4. Так как и имеют непрерывные границы, то они измеримы, а, следовательно, имеют площадь, т.е. квадратируемы.

5. Пусть поле задано двумя функциями: . Смешанные производные непрерывны в , т.е. на выполняется равенство . При всех указанных условиях справедлива следующая формула:

. (5)

Доказательство. Изобразим области и (рис. 23).

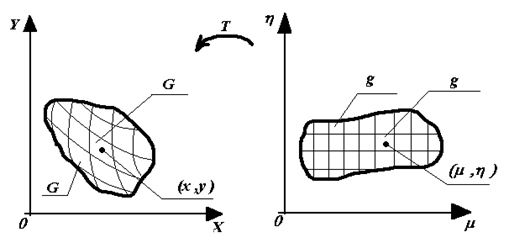
Разобьем область сетью кусочно-гладких кривых на частичные области , , 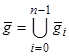причем каждая область имеет кусочно-гладкую границу [25].

Преобразование порождает разбиение области на частичные подобласти с помощью конечного числа кусочно–гладких кривых 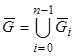[25].

Между областями и существует простая связь:

а) они имеют кусочно–гладкие границы, следовательно, границы непрерывны и области измеримы;

б) частичные области имеют площади, т.е. они квадратируемы и

[25].

Это равенство будет получено при рассмотрении криволинейного интеграла и доказано. Площадь криволинейного частичного прямоугольника равна площади прямоугольника, умноженной на якобиан.

При исследовании определенного интеграла составляли интегральную сумму. Составим и в данном случае сумму вида

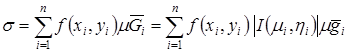. (6)

Так как точка выбрана произвольно в области , то можно принять, что .

При таком условии правая часть интегральной суммы примет вид:

.

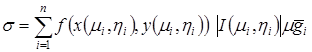Если меру площади устремить к 0, то в пределе получим двойной интеграл по области :. Переходя к пределу в левой части выражения (6) при , получим двойной интеграл [25].

Значит, справедливость формулы (5) доказана. Существует предел от левой и правой частей интегральной суммы, так как функция непрерывна по области и непрерывным является каждый из сомножителей и в .

Замечание. Устремление меры площади к 0 приводит к устремлению к 0 наибольшего диаметра частичных областей, т.е. , – наибольший диаметр частичной области и , –наибольший диаметр частичной области .

Результатом выпускной квалификационной работы являются разработанные методические рекомендации к проведению лекционных и практических занятий по теме «Двойной интеграл», конспект фондовых лекций, обучающе-контролирующая программа.

При разработке лекционных и практических занятий соблюдались основные принципы дидактики: принцип наглядности, принцип научности, принцип систематичности и последовательности, принцип доступности, принцип связи теории с практикой.

Разработанные методики были апробированы на втором курсе факультета математики и информатики СГПИ в феврале – марте 2003–2004 учебного года. Также с целью выявления направленности учебной мотивации было проведено анкетирование, результаты которого учитывались при апробации. Результаты апробации показали, что новые образовательные технологии (в данном случае, педагогика сотрудничества и информационные технологии) целесообразно применять на занятиях по математическому анализу.

При разработке практических занятий и создании компьютерной программы учитывались психологические особенности студенческого возраста.

Материалы выпускной квалификационной работы будут полезны студентам второго курса математического факультета педагогического вуза, желающим расширить и систематизировать свои знания по теме «Двойной интеграл», а также при самостоятельном изучении темы. В разработанных практических занятиях подробно рассматриваются методы решения всех основных типов задач на вычисление двойного интеграла, что позволит студентам лучше разобраться в сложных для них вопросах.

Кроме того, результаты исследования будут полезны преподавателям при подготовке и проведении лекционных занятий, поскольку содержат рекомендации к применению новейших информационных технологий; и практических занятий, так как включают в себя практические рекомендации по использованию метода сотрудничества на занятиях по математическому анализу.