Разработка методики обучения интегрального исчисления функции двух переменных

А преобразование области в – как переход от прямоугольной декартовой системы координат к криволинейной системе координат ight=21 src="images/referats/27477/image251.png">с помощью систем уравнений , где каждая точка .

Значит, любая точка области имеет две пары координат: прямоугольные декартовы и криволинейные.

Полярная система координат

Простейшим и важнейшим примером криволинейных координат являются полярные координаты . Они имеют наглядное геометрическое истолкование, как полярный радиус-вектор и полярный угол, но могут быть введены и формально, с помощью известных соотношений:

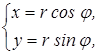
где . Если значения и откладывать по двум взаимно перпендикулярным осям, считая, например, – абсциссой, а – ординатой (при правой ориентации осей), то каждой точке полуплоскости по указанным формулам отвечает одна определенная точка на плоскости [1].

В этом случае координатные линии имеют вид: прямым , отвечают круги радиуса с центром в начале координат, а прямым отвечают лучи, исходящие из начала координат под углом к оси .

Однако в данном случае формулы преобразования, вообще, не будут однозначно разрешимы: изменение величины угла на (где – целое) не отразится на значениях и . Для того, чтобы получить все точки плоскости , достаточно ограничиться значениями , [1].

Каждой точке , отличной от начала, отвечает одно значение и одно значение в указанных пределах. Но неустранимое нарушение однозначности соответствия связано с началом координат: точке отвечает на плоскости вся ось (или ее отрезок от до ).

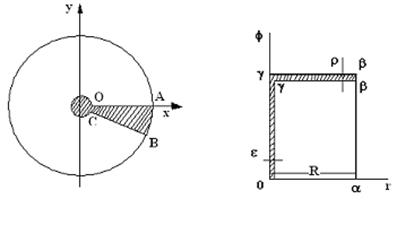
Рассмотрим на плоскости замкнутый прямоугольник или (рис. 22); легко видеть, что на плоскости ему отвечает замкнутый круг, описанный вокруг начала 0 радиусом R=OA. Но весь контур этого круга отвечает одной лишь стороне упомянутого прямоугольника; сторонам и (обеим!) отвечает один и тот же радиус ОА круга; наконец, всей стороне отвечает лишь точка О. Здесь явно не соблюдены указанные в предыдущем пункте условия. (радиуса ) и отрезок ОА

Однако если сдвинуть сторону на малую величину , а сторону на , то новому прямоугольнику будет отвечать на плоскости фигура , полученная из круга удалением малого круга радиусом и сектора с центральным углом , с соблюдением уже всех требований. При перемещении точки на плоскости по отрезкам соответствующая точка на плоскости Oxy опишет по порядку неполную окружность C’O (радиуса r) и отрезок ОА.

Найдем первые частные производные функций :

.

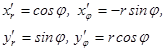Найдем якобиан: 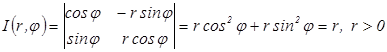, т.е. Якобиан сохраняет положительный знак [1].

Прямые уравнения, связывающие прямоугольную декартову систему координат с полярной системой координат, имеют вид: .

Обратные уравнения, связывающие полярную систему координат с прямоугольной декартовой системой координат, имеют вид:

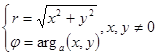[1].

Замена переменных в двойном интеграле

1. Пусть функция непрерывна в замкнутой области с кусочно-гладкой границей.