Разработка методики обучения интегрального исчисления функции двух переменных
Будем предполагать, что функции Значит, определитель Если взять в области Теорема. Пусть Т – преобразование области Доказательство. Ограничимся гладким куском кривой, так как для кусочно-гладкой кривой доказательство будет аналогичным.
Пусть уравнения кривой причем так как кривая Подставляя эти функции в формулы преобразования (3), получим параметрические уравнения соответствующей кривой Легко видеть, что эти функции также имеют непрерывные производные: Криволинейная система координат
Преобразования областей для удобства трактуют как переход от прямоугольной декартовой системы координат к криволинейной системе координат [42].
Пусть поле Координатная сетка в плоскости При преобразовании Они образуют сеть гладких кривых в области Так как поле Эти координатные кривые линии сопоставляют точке с координатами Полагая в (4) (роль параметра здесь играет Аналогично при Имея криволинейные координаты ![]() и
и ![]() не только непрерывны в соответствующих областях, но и имеют непрерывные частные производные (первого порядка)
не только непрерывны в соответствующих областях, но и имеют непрерывные частные производные (первого порядка) ![]() , что частные производные второго порядка (смешанные)
, что частные производные второго порядка (смешанные) ![]() , что функциональный определитель (равный якобиану поля Т)
, что функциональный определитель (равный якобиану поля Т) 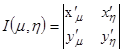 отличен от нуля всюду на области
отличен от нуля всюду на области ![]() .
.
![]() – непрерывен на области
– непрерывен на области ![]() , так как состоит из непрерывных функций и сохраняет постоянный знак [1].
, так как состоит из непрерывных функций и сохраняет постоянный знак [1].
![]() простую кусочно-гладкую кривую
простую кусочно-гладкую кривую ![]() , то с помощью преобразования
, то с помощью преобразования ![]() она перейдет в подобную же кривую
она перейдет в подобную же кривую ![]() в области
в области ![]() [1].
[1].
![]() в область
в область ![]() . Тогда кусочно-гладкая кривая, принадлежащая области
. Тогда кусочно-гладкая кривая, принадлежащая области ![]() , перейдет в кусочно-гладкую кривую, принадлежащую области
, перейдет в кусочно-гладкую кривую, принадлежащую области ![]() [1].
[1].
![]() будут:
будут:
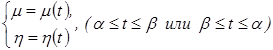 ,
,
![]() гладкая, можно функции
гладкая, можно функции ![]() считать имеющими непрерывные производные на отрезке
считать имеющими непрерывные производные на отрезке ![]() , не обращающиеся одновременно в ноль.
, не обращающиеся одновременно в ноль.
![]() :
:
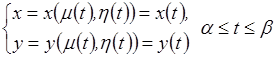 .
.
![]() , (так как
, (так как ![]() непрерывны на
непрерывны на ![]() ), которые к тому же не могут одновременно обратиться в ноль. Следовательно, кривая
), которые к тому же не могут одновременно обратиться в ноль. Следовательно, кривая ![]() – гладкая кривая [1].
– гладкая кривая [1].
![]() преобразует область
преобразует область ![]() плоскости
плоскости ![]() в область
в область ![]() плоскости
плоскости ![]() .
.
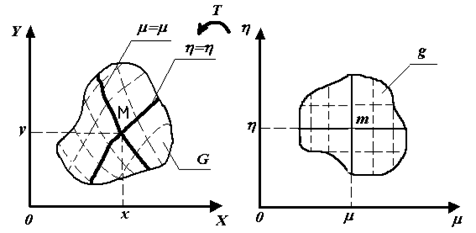
![]() наводит координатную сеть в области
наводит координатную сеть в области ![]() :
: ![]() . Координатные линии параллельны осям
. Координатные линии параллельны осям ![]() и
и ![]() .
.
![]() эти прямые (частный случай гладкой кривой) переходят в гладкие кривые в области
эти прямые (частный случай гладкой кривой) переходят в гладкие кривые в области ![]() (в соответствии с доказанной в предыдущем пункте теоремой).
(в соответствии с доказанной в предыдущем пункте теоремой).
![]() и называются криволинейными координатными линиями (координатные прямые области
и называются криволинейными координатными линиями (координатные прямые области ![]() порождают координатные кривые области
порождают координатные кривые области ![]() ) [42].
) [42].
![]() взаимно однозначно, то через каждую точку
взаимно однозначно, то через каждую точку ![]() проходят только две координатные криволинейные линии, которые являются образами линий
проходят только две координатные криволинейные линии, которые являются образами линий ![]() .
.
![]() два числа
два числа ![]() , которые называются криволинейными координатами точки
, которые называются криволинейными координатами точки ![]() . Криволинейные координаты
. Криволинейные координаты ![]() точки
точки ![]() связаны с прямоугольной декартовой системой координат прямыми уравнениями
связаны с прямоугольной декартовой системой координат прямыми уравнениями ![]() и обратными уравнениями
и обратными уравнениями ![]() .
.
![]() , получим параметрическое представление координатной линии:
, получим параметрическое представление координатной линии:
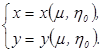
![]() ). Неявное уравнение той же линии получим, полагая
). Неявное уравнение той же линии получим, полагая ![]() во втором из уравнений (4).
во втором из уравнений (4).
![]() , получим следующее параметрическое представление координатной линии:
, получим следующее параметрическое представление координатной линии:
![]()
![]() , можно трактовать преобразование
, можно трактовать преобразование ![]() областей как переход в
областей как переход в ![]() от криволинейных координат
от криволинейных координат ![]() к прямоугольной декартовой системе координат
к прямоугольной декартовой системе координат ![]() .
.
Другие рефераты на тему «Педагогика»:
Поиск рефератов
Последние рефераты раздела
