Разработка методики обучения интегрального исчисления функции двух переменных
![]() .
.
Введем вспомогательную функцию 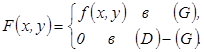
Функция ![]() удовлетворяет всем условиям предыдущей теоремы:
удовлетворяет всем условиям предыдущей теоремы:
1) интегрируема в области ![]() , так к
, так к
ак ![]()
2) интегрируема в области ![]() , так как
, так как ![]() =0.
=0.
На основании одного из свойств двойного интеграла:![]() , и условия, что функция
, и условия, что функция ![]() интегрируема на области
интегрируема на области ![]() , получаем:
, получаем:
![]() .
.
По условию теоремы для всех ![]() существует определенный интеграл
существует определенный интеграл 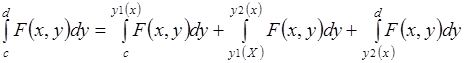 , так как существует каждый из трех определенных интегралов справа.
, так как существует каждый из трех определенных интегралов справа.
Действительно, на отрезках ![]() и
и ![]() областей вне области
областей вне области ![]() значение функции равно нулю.
значение функции равно нулю.
Следовательно, первый и третий интегралы существуют и равны нулю, а второй интеграл существует по условию теоремы, так как ![]() в области
в области ![]() . Следовательно,
. Следовательно, 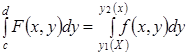 .
.
Таким образом, для функции ![]() выполняются все условия предыдущей теоремы.
выполняются все условия предыдущей теоремы.
Значит, и двойной интеграл от функции ![]() –
–![]() может быть сведен к повторному:
может быть сведен к повторному: 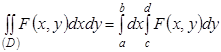 .
.
Замечание. Если в данной теореме поменять ролями переменные х и у, то теорема будет утверждать существование следующего повторного интеграла:
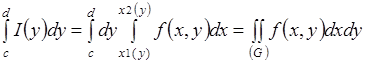 [1].
[1].
2.3 Замена переменных в двойном интеграле
Преобразование областей при регулярных отображениях
Этот раздел посвящен задаче преобразования двойного интеграла
![]()
с помощью замены переменных вида ![]() .
.
Окажется, что ![]() и
и ![]() удобно рассматривать как компоненты отображения некоторого открытого подмножества плоскости с координатами
удобно рассматривать как компоненты отображения некоторого открытого подмножества плоскости с координатами ![]() в координатную плоскость с координатами
в координатную плоскость с координатами ![]() [33].
[33].
Если ![]() – некоторая замкнутая область, то будем обозначать
– некоторая замкнутая область, то будем обозначать ![]() – ее границу,
– ее границу, ![]() – область вместе с границей, то есть
– область вместе с границей, то есть ![]() .
.
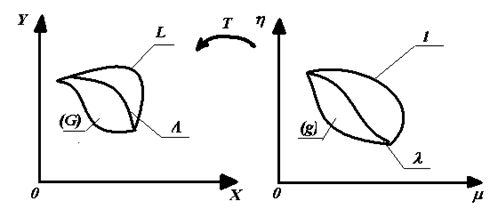
Рассмотрим две плоскости ![]() и в них исследуем две замкнутые области
и в них исследуем две замкнутые области ![]() и
и ![]() . Каждая из этих областей может быть и неограниченной, в частности может охватывать и всю плоскость. Контур или границу области (если область не охватывает всей области) будем предполагать кусочно-гладкой кривой.
. Каждая из этих областей может быть и неограниченной, в частности может охватывать и всю плоскость. Контур или границу области (если область не охватывает всей области) будем предполагать кусочно-гладкой кривой.
Пусть ![]() и
и ![]() соответственно – границы указанных областей.
соответственно – границы указанных областей.
Допустим, что в области ![]() дана система непрерывных функций:
дана система непрерывных функций:
![]() (3)
(3)
которая каждой точке ![]() области
области ![]() относит одну определенную точку
относит одну определенную точку ![]() области
области ![]() , причем ни одна точка
, причем ни одна точка ![]() из
из ![]() не будет пропущена, так что каждая такая точка отнесена хоть одной точке
не будет пропущена, так что каждая такая точка отнесена хоть одной точке ![]() из
из ![]() . Если различным точкам
. Если различным точкам ![]() отвечают различные же точки
отвечают различные же точки ![]() , так что каждая точка
, так что каждая точка ![]() отнесена лишь одной точке
отнесена лишь одной точке ![]() , то формулы (3) однозначно разрешимы относительно
, то формулы (3) однозначно разрешимы относительно ![]() . Переменные
. Переменные ![]() в свою очередь являются однозначными функциями от
в свою очередь являются однозначными функциями от ![]() в области
в области ![]() :
:
![]() (4)
(4)
Таким образом, между областями ![]() и
и ![]() устанавливается взаимно-однозначное соответствие. Говорят также, что формулы (3) осуществляют преобразование
устанавливается взаимно-однозначное соответствие. Говорят также, что формулы (3) осуществляют преобразование![]() области
области ![]() в область
в область ![]() , а формулы (4) дают преобразование
, а формулы (4) дают преобразование ![]() области
области ![]() в область
в область ![]() .
.
Если названные области заполняют соответствующие плоскости, то имеем дело с преобразованием одной плоскости в другую.
Другие рефераты на тему «Педагогика»:
- Принцип межпредметных связей при решении химических задач. Разбор основных способов решения расчетных задач
- Проблемы обучения детей на занятиях в условиях разновозрастной группы
- Формирование читательской деятельности учащихся первого класса на уроках внеклассного чтения
- Коррекционная направленность педагогической работы по формированию грамматического строя речи у детей с трудностями в обучении
- Обучение чтению на уроках английского языка в начальной школе
Поиск рефератов
Последние рефераты раздела
- Тенденции развития системы высшего образования в Украине и за рубежом: основные направления
- Влияние здоровьесберегающего подхода в организации воспитательной работы на формирование валеологической грамотности младших школьников
- Характеристика компетенций бакалавров – психологов образования
- Коррекционная программа по снижению тревожности у детей младшего школьного возраста методом глинотерапии
- Формирование лексики у дошкольников с общим недоразвитием речи
- Роль наглядности в преподавании изобразительного искусства
- Активные методы теоретического обучения
