Разработка методики обучения интегрального исчисления функции двух переменных

,

откуда и следует выполнение необходимого и достаточного условия интегрируемости функции двух переменных. Этим интегрируемость функции доказана [1].

Основные свойства двойного интеграла

10. Если область , в которой задана непрерывная функция 57 height=25 src="images/referats/27477/image016.png">, непрерывной кривой разложена на две области и , то из интегрируемости функции во всей области следует ее интегрируемость в частичных областях и , и обратно – из интегрируемости функции в обеих областях и вытекает интегрируемость в области . При этом

. (1)

Доказательство. Разобьем области и на части. Это разбиение порождает разложение всей области на части, причем

(1*)

Так как непрерывна на , то она интегрируема на , и следовательно, существует предел от левой части выражения (1*), следовательно, будут существовать и пределы каждой части справа.

Перейдем к пределу при в выражении (1*) и получим формулу (1) [1].

20. Если умножить интегрируемую в области функциюна постоянную , то полученная функция также будет интегрируема в (Р), и при этом

Доказательство. Если перейти к пределу при в верном равенстве

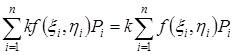, то получим нужную формулу [1].

30. Если в области интегрируемы функции и , то интегрируема и функция , причем

.

Доказательство. Свойство доказывается при предельном переходе при в верном равенстве

[1].

40. Если для интегрируемых в области функций и выполняется неравенство , то

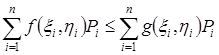Доказательство. Доказательство основано на предельном переходе при в верном неравенстве [1].

50. В случае интегрируемости функции в области (Р) интегрируема и функция , и имеет место неравенство

.

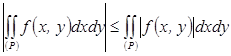Доказательство. Пусть S' и s' верхняя и нижняя суммы Дарбу на области (Р) для функции |f (x, y)|, а S и s – верхняя и нижняя суммы Дарбу для функции f (x, y).

Составим разность S'-s' для функции |f (x, y)|:

,

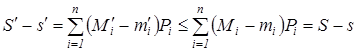так как .

При λ→0 разность S-s стремится к нулю, так как функция f (x, y) интегрируема на (Р) по условию, а, значит, и S'-s' стремится к нулю при λ→0 подавно.

Так как S'-s' стремится к нулю при λ→0, то функция |f (x, y)| интегрируема на (Р).

При λ→0 в очевидном неравенстве 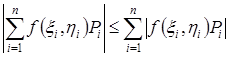переходим к пределу и получаем формулу свойства [1].

Теорема о среднем значении

Теорема 1. Если функция интегрируема в замкнутой области (P) и выполняется неравенство , то:

1. Справедливо неравенство , где m, M – наименьшее и наибольшее значения функции в области (P), а P площадь области (P).

2. Существует такая точка с из отрезка , что выполняется:

Доказательство. 1. Первое утверждение теоремы получается при предельном переходе в двойном неравенстве

2. Пусть некоторая точка с имеет значение .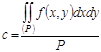

3. Разделим двойное неравенство пункта 1 на Р. Получим

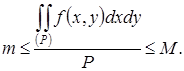
4. С учетом пункта 2 из того, что следует, что и

[1].

Теорема 2. Если функция двух переменных непрерывна на замкнутой области (P), то существует такая точка , что будет выполняться: