Основные понятия космической геодезии и астрономии

Рефераты / Астрономия, авиация и космонавтика / Основные понятия космической геодезии и астрономии

На движение близких к планете спутников большое влияние оказывает также отклонение её формы от сферической.

Особенностью движения Луны является то обстоятельство, что её орбита расположена целиком вне сферы действия тяготения Земли, т. е. за пределами той области, где притяжение Земли преобладает над притяжением Солнца. Поэтому при построении теории движения Луны приходится осуществлять бол

ьше последовательных приближений, чем в планетных задачах. В современной теории движения Луны за первое приближение принимается не задача двух тел, а так называемая задача Хилла - специальный случай задачи трёх тел (обычно под ограниченной задачей трёх тел понимают изучение движения материальной точки P3 под действием притяжения точками P1 и P2 ; точки P1 и P2 движутся по кеплеровским орбитам; точка P3 может иметь и не плоское движение и её действие на точки P1 и P2 не учитывается; масса материальной точки P3 принимается равной нулю), решение которой даёт промежуточную орбиту, более удобную для проведения процесса последовательных приближений, чем эллипс.

Построение математических теорий движения конкретных небесных тел как естественных, так и искусственных (планет, спутников, комет, космических зондов).

Орбиты небесных тел - траектории, по которым движутся небесные тела в космическом пространстве. Формы орбит небесных тел и скорости, с которыми по ним движутся небесные тела, определяются силой тяготения, а также силой светового давления, электромагнитными силами, сопротивлением среды, в которой происходит движение, приливными силами, реактивными силами (в случае движения ядра кометы) и многое др.

В движении планет, комет и спутников планет, а также в движении Солнца и звёзд в Галактике решающее значение имеет сила всемирного тяготения. На активных участках орбит искусственных космических объектов наряду с силами тяготения определяющее значение имеет реактивная сила двигательной установки. Ориентация орбиты в пространстве, её размеры и форма, а также положение небесного тела на орбите определяются величинами (параметрами), называемыми элементами орбиты.

Элементы орбит планет, комет и спутников определяются по результатам астрономических наблюдений в три этапа:

вычисляются элементы т. н. предварительной орбиты без учёта возмущений, т. е. решается задача двух тел. Для этой цели в большинстве случаев достаточно иметь три наблюдения (т. е. координаты трёх точек на небесной сфере) небесного тела (например, малой планеты), охватывающие промежуток времени в несколько дней или недель.

Осуществляется улучшение предварительной орбиты (т. е. вычисляются более точные значения элементов орбиты) по результатам более длительного ряда наблюдений.

Вычисляется окончательная орбита, которая наилучшим образом согласуется со всеми имеющимися наблюдениями.

Для многих тел Солнечной системы, в том числе для больших планет, Луны и некоторых спутников планет, имеются уже длительные ряды наблюдений. Для вычисления по этим наблюдениям окончательной орбиты (или, как говорят, для разработки теории движения небесного тела) применяются аналитические и численные методы небесной механики.

В результате первого этапа орбита определяется в виде конического сечения (эллипса, иногда также параболы или гиперболы), в фокусе которого находится другое (центральное) тело. Такие орбиты называются невозмущёнными или кеплеровыми, т.к. движение небесного тела по ним происходит по законам Кеплера.

Напомним:

Первый закон Кеплера (Закон эллипсов)

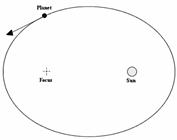
Каждая планета Солнечной системы обращается по эллипсy, в одном из фокусов которого находится Солнце.

Форма эллипса и степень его сходства с окружностью характеризуется отношением

e=\frac{c}{a},

где c — расстояние от центра эллипса до его фокуса (половина межфокусного расстояния), a — большая полуось. Величина e называется эксцентриситетом эллипса. При c = 0 и e = 0 эллипс превращается в окружность.

Закон всемирного тяготения Ньютона гласит, что «каждый объект во вселенной притягивает каждый другой объект по линии соединяющей центры масс объектов, пропорционально массе каждого объекта, и обратно пропорционально квадрату расстояния между объектами». Это предполагает, что ускорение a имеет форму

\mathbf{a} = \frac{d^2\mathbf{r}}{dt^2} = f(r)\hat{\mathbf{r}}.

Вспомним, что в полярных координатах

\frac{d\mathbf{r}}{dt} =\dot r\hat{\mathbf{r}} + r\dot\theta\hat{\boldsymbol\theta},

\frac{d^2\mathbf{r}}{dt^2} = (\ddot r - r\dot\theta^2)\hat{\mathbf{r}} + (r\ddot\theta + 2\dot r \dot\theta)\hat{\boldsymbol\theta}.

В координатной форме запишем

\ddot r - r\dot\theta^2 = f(r),

r\ddot\theta + 2\dot r\dot\theta = 0.

Подставляя \ddot \thetaи \dot rво второе уравнение, получим

r { d \dot\theta \over dt } + 2 {dr \over dt} \dot\theta = 0,

которое упрощается

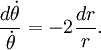
\frac{d\dot\theta}{\dot\theta} = -2\frac{dr}{r}.

После интегрирования запишем выражение

\log\dot\theta = -2\log r + \log\ell,

\log\ell = \log r^2 + \log\dot\theta,

\ell = r^2\dot\theta,

для некоторой константы \ell, которая является удельным угловым моментом (\ell=\mathbf{r}\times \mathbf{v}).Пусть

r = \frac{1}{u},

\dot r = -\frac{1}{u^2}\dot u = -\frac{1}{u^2}\frac{d\theta}{dt}\frac{du}{d\theta}= -\ell\frac{du}{d\theta},

\ddot r = -\ell\frac{d}{dt}\frac{du}{d\theta} = -\ell\dot\theta\frac{d^2u}{d\theta^2}= -\ell^2u^2\frac{d^2u}{d\theta^2}.

Уравнение движения в направлении \hat{\mathbf{r}}становится равным

Скачать реферат Скачать реферат
Страница:  1  2  3  4  5  6  7 


Другие рефераты на тему «Астрономия, авиация и космонавтика»:

Поиск рефератов

Последние рефераты раздела

Copyright © 2010-2024 - www.refsru.com - рефераты, курсовые и дипломные работы