Проектирование системы оптимального корректирующего устройства

Из таблицы (см. табл. 1.3) видно, что на частоте расчетная ЛАЧХ заходит в запретную область. Следовательно, ЛАЧХ необходимо поднять на 0,011 дБ. Таким образом, минимальный коэффициент усиления разомкнутой системы будет равен:

с-1.

Коэффиц

иент усиления пропорционального регулятора рассчитывается по формуле:

.

Структурная схема системы с пропорциональным регулятором с числовыми параметрами изображена на рис. 1.7.

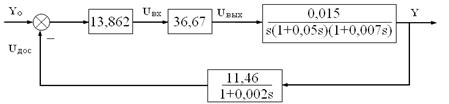
Рис. 1.7. Структурная схема системы с пропорциональным регулятором

1.2.2 Проверка устойчивости замкнутой системы

Проверим устойчивость системы по алгебраическому критерию Гурвица (см. п.1.1).

ХУ ЗС: ,

,

,

,

; ; ; ; .

Необходимое условие устойчивости выполняется, так как .

Проверим достаточное условие устойчивости. Для системы четвертого порядка достаточно проверить выполнение условия:

,

,

.

Условие выполняется, следовательно, система устойчива.

Проверим устойчивость системы по критерию Найквиста [1, §6.5, §6.6].

1. С использованием амплитудно-фазовой частотной характеристики (АФЧХ):

Запишем ПФ РС:

.

Для того чтобы судить об устойчивости замкнутой системы, необходимо проверить устойчивость разомкнутой системы. Для этого запишем характеристическое уравнение разомкнутой системы (ХУ РЗ) и найдем корни уравнения:

,

; ; ; .

Так как один из корней равен нулю (), а все остальные корни с отрицательными вещественными частями (левые), то можно сделать вывод, что разомкнутая система находится на апериодической границе устойчивости.

Далее необходимо построить АФЧХ разомкнутой системы (годограф Найквиста). Запишем выражение для построения АФЧХ и выделим действительную и мнимую части:

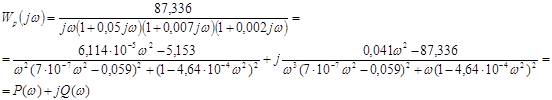
Задаваясь различными значениями ω в пределах от нуля до бесконечности, построим годограф Найквиста (рис. 1.8) по характерным точкам (табл. 1.4):

Таблица 1.4

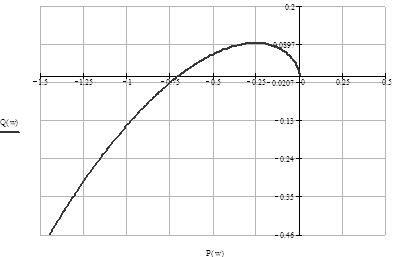
Рис. 1.8. Годограф Найквиста

Так как годограф Найквиста, дополненный на участке разрыва дугой бесконечно большого радиуса, не охватывает особую точку (−1;j0), то замкнутая система устойчива.

2. С использованием ЛЧХ:

Запишем выражения и построим ЛАЧХ и ЛФЧХ (рис. 1.9):

.

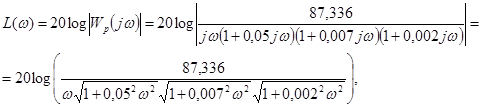
Рис. 1.9. ЛЧХ системы

Замкнутая система устойчива, если выполняется неравенство:

,

где – частота среза, при которой ;

– критическая частота, при которой .

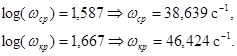
Так как неравенство выполняется, следовательно, замкнутая система устойчива.

Проверим устойчивость системы по критерию Михайлова [1, §6.3].

Запишем ХУ ЗС:

,

,

,

.

Подставим в этот полином чисто мнимое значение . При этом получим функцию Михайлова, как характеристический полином, состоящий из вещественной и мнимой части:

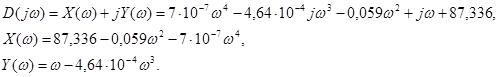
Задаваясь различными значениями ω в пределах от нуля до бесконечности, построим годограф Михайлова (рис. 1.10) по характерным точкам (табл. 1.5):

Таблица 1.5

 Скачать реферат