Вероятностные процессы и математическая статистика в автоматизированных системах

4.5 Вызов и загрузка

Для инсталляции программы необходимо выполнить следующие шаги:

1) убедиться в том, что компьютер, на который устанавливается система, отвечает всем требованиям, изложенным в разделе «Минимальные системные требования»;

2) убедиться в исправности накопителей на гибких магнитных носителях;

3) перекопировать программу на жесткий диск компьютера; <

p>4) запустить файл Rgr.exe.

4.6 Входные данные

Входными данными к программе являются:

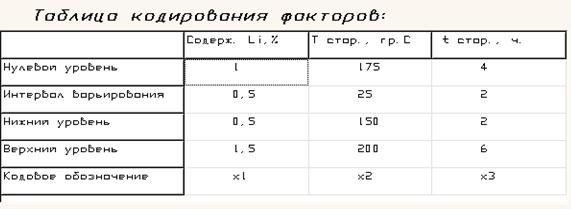
1) таблица кодирования (таблица 1);

2) результаты экспериментов.

Входные данные заданы в программе.

4.7 Выходные данные

Выходными данными являются:

1) дисперсии опытов;

2) коэффициенты линии регресии;

3) расчетные значения выходов;

4) заключения о воспроизводимости опытов, значимости коэффициентов модели, адекватности модели;

5) графики отклика при двух постоянных значениях факторов;

6) кривые равного выхода при одном постоянном факторе;

7) наилучшие и наихудшие сочетания факторов.

5. Результаты обработки данных эксперимента

В результате работы программы были получены следующие результаты:

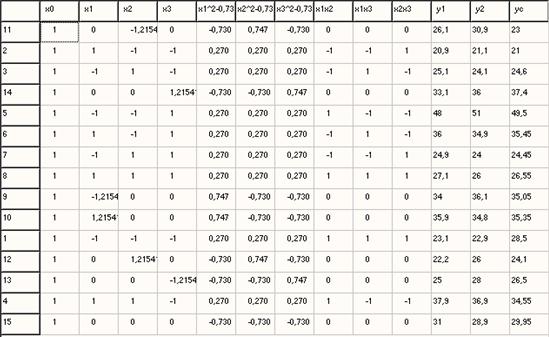
Расширенная план-матрица эксперимента

Нахождение коэффициентов, проверка их значимости и анализ полученной модели показано на рисунке 3.

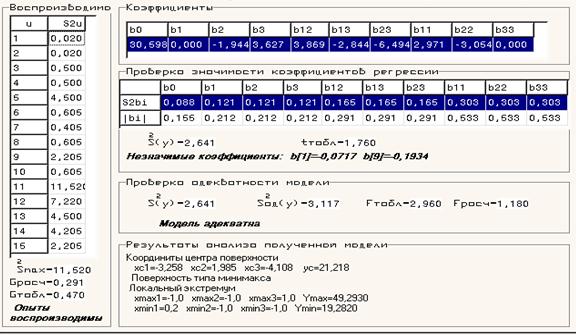
Рисунок 3 – Результат работа программы

6. графики зависимости отклика

Графики зависимости отклика от каждого из параметров представлены на рисунка 4-6.

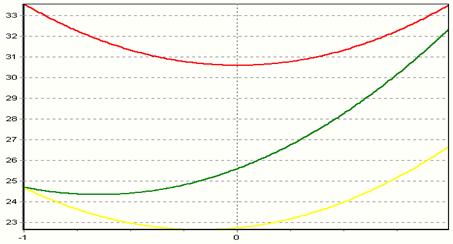
Рисунок 4 – зависимость отклика от изменения параметра x1. Зависимость отклика от X1

y= 30,60 + 0,00*x1 + 2,97*x1^2 x2=0 x3=0

y= 25,60 + 3,87*x1 + 2,97*x1^2 x2=1 x3=0

y= 22,73 + 1,02*x1 + 2,97*x1^2 x2=1 x3=1

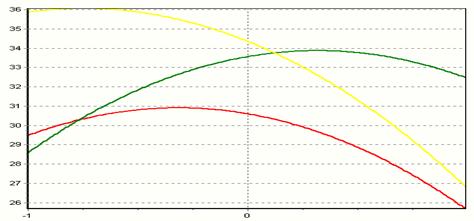
Рисунок 5 - зависимость отклика от изменения параметра x2. Зависимость отклика от X2

y= 30,60 + -1,94*x2 + -3,05*x2^2 x1=0 x3=0

y= 33,57 + 1,92*x2 + -3,05*x2^2 x1=1 x3=0

y= 34,35 + -4,57*x2 + -3,05*x2^2 x1=1 x3=1

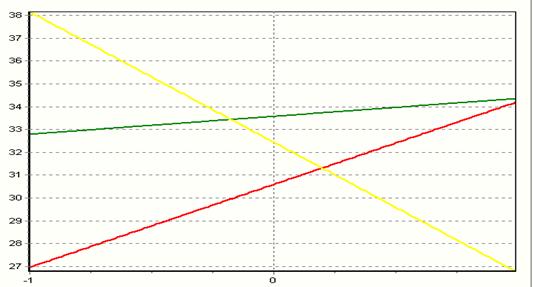
Рисунок 6 - зависимость отклика от изменения параметра x3. Зависимость отклика от X3

y= 30,60 + 3,63*x3 + 0,00*x3^2 x1=0 x2=0

y= 33,57 + 0,78*x3 + 0,00*x3^2 x1=1 x2=0

y= 32,44 + -5,71*x3 + 0,00*x3^2 x1=1 x2=1

7. кривые равного выхода

Графики зависимости отклика от каждого из параметров представлены на рисунках 7-9

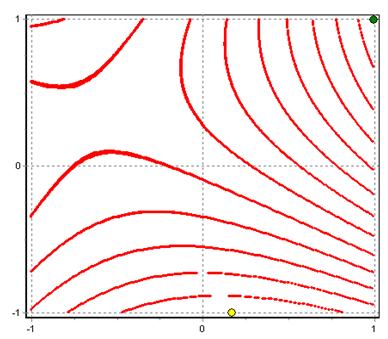
Рисунок 7 – Линии уровня отклика при фиксированном x3

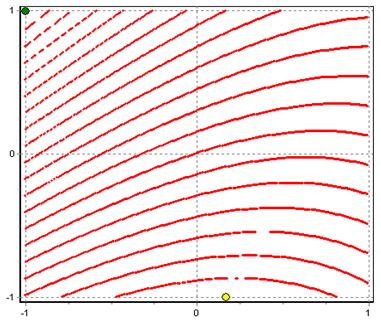
Рисунок 8 – Линии уровня отклика при фиксированном x2

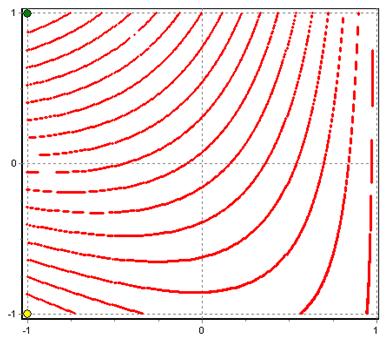
Рисунок 9 – Линии уровня отклика при фиксированном x1

Заключение

В ходе выполнения данной расчетно-графической работы был определен оптимальный предел прочности алюминиевых деформируемых сплавов, определяющийся при испытании на растяжение.

Оптимальный параметры прочности:

Содержание Li(%) = 0.6

Температура старения(град.С)=25

Время старения(час.)=2

Содержание Li(%) = 0.6

Температура старения(град.С)=25

Время старения(час.)=2

Содержание Li(%) = 1.5

Температура старения(град.С)=200

Время старения(час.)=6

список использованных источников

1) Конспект лекций по дисциплине «ВП и МСАС».

2) Конспект лекций по дисциплине «ТА и МОПЗ».

3) Конспект лекций по дисциплине «Методы синтеза и оптимизации».

4) Методические указания к лабораторным и расчетно-графической работе по дисциплине "Вероятностные процессы и математическая статистика в автоматизированных системах" / Сост.:Г.Б.Билык, О.В.Веремей, В.И.Кравченко. - ДГМА, 2006. - 24 с. (файл VPLAB).

5) Применение математических методов и ЭВМ. Планирование и обработка результатов эксперимента / Под ред. А.Н. Останина. - Мн.: Выш. шк., 2005. - 218 с.

приложение

Листинг модуля Metod.pas – подпрограммы общего назначения

type mas=array[1 3] of real;

var x:array[0 9,1 15] of real;

x2:array[1 3,1 15] of real;

x0,ix,xc,la,m,l,n,ml,nl,

xp1,xp2,xp3,xh,xlocmax,xlocmin:mas;

y,ys:array[1 2,1 20] of real;

x12,x23,x13,yc,ycs,s2u:array[1 15] of real;

b,s2b,db:array[0 9] of real;

kk:integer;

d,xc2,S2UMax,s2y,ycen,ylocmax,ylocmin:real;

{$R *.dfm}

function sx(l:integer):real;

var s:real; i:integer;

begin s:=0;

for i:=1 to 15 do

s:=s+sqr(x[l,i]);

sx:=s;

end;

function sxy(l:integer):real;

var s:real; i:integer;

begin s:=0;

for i:=1 to 15 do

s:=s+x[l,i]*yc[i];

sxy:=s;

end;

function f(l:integer):real;

var xx1,xx2,xx3:real;

begin

xx1:=x[1,l]; xx2:=x[2,l]; xx3:=x[3,l];

f:=b[0]+b[1]*xx1+b[2]*xx2+b[3]*xx3

+b[4]*xx1*xx2+b[5]*xx1*xx3+b[6]*xx2*xx3+

b[7]*xx1*xx1+b[8]*xx2*xx2+b[9]*xx2*xx2;

end;

function fy(xx1,xx2,xx3:real):real;

begin

fy:=b[0]+b[1]*xx1+b[2]*xx2+b[3]*xx3

+b[4]*xx1*xx2+b[5]*xx1*xx3+b[6]*xx2*xx3+

b[7]*xx1*xx1+b[8]*xx2*xx2+b[9]*xx2*xx2;

end;

function dlambda(lam:real):real;

begin dlambda:=(b[7]-lam)*((b[8]-lam)*(b[9]-lam)-0.25*b[6]*b[6])-

0.5*b[4]*(0.5*b[4]*(b[9]-lam)-0.25*b[5]*b[6])+

0.5*b[5]*(0.25*b[4]*b[6]-0.5*b[5]*(b[8]-lam))

end;

function findl(xa,xb:real):real;

var c:real;

begin

repeat

c:=(xa+xb)/2;

if dlambda(xa)*dlambda(c)<0 then xb:=c

else xa:=c;

until abs(dlambda(xa)-dlambda(xb))<=0.001;

findl:=(xa+xb)/2;

end;

procedure maximminim;

var yt:array[1 2,1 2,1 2] of real; i,j,w:integer;

minim,maxim:real;

begin minim:=fy(1,1,1);

maxim:=fy(1,1,1);

for i:=-10 to 10 do

for j:=-10 to 10 do

for w:=-10 to 10 do

begin if fy(i/10,j/10,w/10)>=maxim then begin

maxim:=fy(i/10,j/10,w/10); xlocmax[1]:=i/10;

xlocmax[2]:=j/10; xlocmax[3]:=w/10; end;

if fy(i/10,j/10,w/10)<=minim then begin

minim:=fy(i/10,j/10,w/10);xlocmin[1]:=i/10;

xlocmin[2]:=j/10; xlocmin[3]:=w/10; end;

end;

ylocmin:=minim;

ylocmax:=maxim;

end;

procedure minmax;

type arr=array [1 3,1 3] of real;

var d,d1,d2,d3:arr; i:integer; bd:mas;

function delta(a:arr):real;

begin delta:=a[1,1]*(a[2,2]*a[3,3]-a[2,3]*a[3,2])-

a[1,2]*(a[2,1]*a[3,3]-a[2,3]*a[3,1])+

a[1,3]*(a[2,1]*a[3,2]-a[2,2]*a[3,1]); end;

begin d[1,1]:=2*b[7]; d[1,2]:=b[4]; d[1,3]:=b[5];

 Скачать реферат