Геометрические задачи, приводящие к дифференциальным уравнениям

dA λdL,

или

dA λdL 0.

Это приводит к теореме:

Как бы мы не изменили кривую y = f(x), изменяя ее длину или нет, величина dAλdL никогда не является положительной. Но если dAλdL не положительно, то АλL не может быть больше для новой кривой, чем для прежней. Мы можем, следовательно, высказать полученную теорему в более выразительной форме:

Кривая, для которой величина А наибольшая по сравнению с кривыми той же длины, делает наибольшей величину АλL. по сравнению с кривыми произвольной длины.

Поэтому решить задачу максимума для А с ограничением, что длина кривых сравнения L , равна Lo, — то же самое, что решить задачу максимума для АλL без всяких ограничений на кривые сравнения. Правда, правильное решение задачи получится только в том случае, если λ выбрана правильно, а так как невозможно определить λ, не зная решения задачи, то может показаться, что мы ничего не достигли нашим рассуждением.

Мы увидим, однако, что, предполагая пока λ неизвестной постоянной, мы найдем в дальнейшем способ ее определения. Итак, интеграл, максимум которого требуется найти, есть:

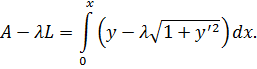
Обычные преобразования приводят к дифференциальному уравнению:

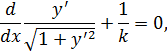
решение которого

+=λ

Это — уравнение круга, радиуса λ, с центром в точке (α, β). В него входят три произвольных постоянных α, β и λ, но мы имеем три условия для их определения, так как кривая должна проходить через точки (0,0), (X, 0) и должна иметь длину L.

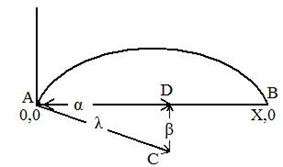
Простейший способ определения постоянных— геометрический. Известно, что центр круга, проходящего через две точки А и В, лежит на перпендикуляре, делящем хорду АВ пополам. Отсюда а равняется . Так как гипотенуза и один из катетов треугольника ADC известны, то легко вычислить другой катет.

Итак, получаем для β значение . Наконец, есть величина угла АС В, измеренного в радианах. Угол ACD равен половине этого угла, и его синус равен

Это дает нам уравнение:

откуда можно определить λ. Уравнение трансцендентное и его нельзя решить алгебраическим методом. Его можно решить приближенно путем догадки или с помощью рядов. Так, например, если L равно 1,25 X, λ оказывается равным , а следовательно, β=-0,234Х. Это как раз тот круг, который изображен на рисунке.

Заключение

Данная курсовая работа состоит из введения, основной части, заключения и списка использованной литературы.

Целью курсовой работы являться рассмотрение геометрических задач и приведение их к дифференциальным уравнениям.

В ходе выполнения данной курсовой работы мы пришли к тому, что часть дифференциальных уравнений разрешимы явно, а часть уравнений явно неразрешимы.

Таким образом, из вышесказанного можно сделать вывод, что цель курсовой работы достигнута.

Список использованной литературы

1. Арнольд В. И. Обыкновенные дифференциальные уравнения. – М.: Наука, 1984. – 271 с.

2. Богданов Ю. С. Лекции по дифференциальным уравнениям. – Минск: Вышейшая школа, 1977. – 239 с.

3. Еругин Н. П., Штокало И. З., Бондаренко П. С. И др. Курс обыкновенных дифференциальных уравнений. – Киев: Вища школа, 1974. – 471 с.

4. Краснов М. Л. Обыкновенные дифференциальные уравнения. – М.: Высшая школа, 1983. – 128 с.

5. Матвеев Н. М. Дифференциальные уравнения: Учеб. Пособие для студентов пед. ин-тов по физ.-мат. спец. – М.: Просвещение, 1988. – 256 с.

6. Матвеев Н. М. Сборник задач и упражнений по обыкновенным дифференциальным уравнениям. – Минск: Вышейшая школа, 1987. – 319 с.

7. Матвеев Н. М. Методы интегрирования обыкновенных дифференциальных уравнений. – Минск: Вышейшая школа, 1974. – 766 с.

8. Петровский И. Г. Лекции по теории обыкновенных дифференциальных уравнений. – М.: 1952 Ленинград.

9. Понтрягин Л. С. Обыкновенные дифференциальные уравнения. – М.: Наука, 1970. – 331 с.

10. Самойленко А. М., Кривошея С. А., Перестюк Н. А. Дифференциальные уравнения, примеры и задачи. – Киев: Вища школа, 1984. – 408 с.

11. Смирнов М. М. Дифференциальные уравнения в частных производных второго порядка. – М.: Наука, 1964. – 205 с.

12. Тихонов А. Н., Васильева А. Б., Свешников А. Г. Дифференциальные уравнения. – М.: Наука, 1972. – 724 с.

13. Тихонов А. Н., Самарский А. А. Уравнения математической физики. – М.: Наука, 1972. – 724 с.

14. Торнтон Фрай. Элементарный курс дифференциальных уравнений. – М.: 1933 Ленинград.

15. Федорюк М. В. Обыкновенные дифференциальные уравнения. – М.: Наука, 1979. – 352 с.

[1] Предполагаются различными те линии семейства (2), кото­рым соответствуют различные С.

[2] Она зависит от , высоты в точке A, которую мы можем сделать произ­вольной подходящим выбором начала координат.

[3] На самом деле этот элемент есть приращение длины дуги и обозначается в дифференциальном исчислении через Δs. Однако в физических исследованиях, если такое приращение будет стремиться к нулю, пользуются сразу символом диференциала. Это редко приводит к недоразумениям и часто оказывается олез-ным, давая рассуждению большую наглядность.

[4] Т.е. вес на единицу длины.

[5] Это есть, вместе с тем, наименьшее натяжение для точек кривой, а именно — натяжение внизу, где вертикальная компонента натяжения исчезает.

[6] Мы только предполагали ε и очень малыми. Однако и эти ограничения не необходимы и были сделаны только для упрощения рассуждения.

[7] Если точки О и X слишком близки между собой, то может случиться, что придется протягивать веревку под точками берега вне интервала (OX), и инте­гралы в написанной форме не верны. Мы не будем рассматривать этих случаев; мы будем считать у однозначной функции х.

[8] Мы пишем ΔA вместо dA, так как хотим сохранить последний симво

 Скачать реферат