Геометрические задачи, приводящие к дифференциальным уравнениям

И поэтому dx= λ cos t dt или x= λ sin t+

Таким образом,

.

или

.

Экстремалями являются окружности. Постоянные обычным образом определяется из граничных условий и изопериметрической связи.

Задача разрешима, если дуга окружности длины l, соединяющая точки (a, A) и (b, B), не выходит из полосы axb.

Кривая провеса гибкой нерастяжимой нити

В двух точках и на одном уровне и на расстоянии друг от друга подвешена нить. Требуется найти форму, которую примет эта нить под действием силы тяжести. Пусть кривая на рисунке изображает эту форму, и рассмотрим какой-нибудь элемент длины ds[3].

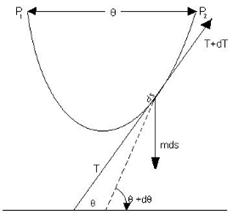
Одно из основных предложений механики состоит в том, что этот элемент должен быть в равновесии под действием сил, действующих на него. Эти силы суть:

a) его собственный вес, являющийся силой, действующей вертикально вниз;

b) натяжение нити в нижнем конце, действующее в направлении касательной в этой точке;

c) натяжение нити в верхнем конце, действующее в направлении касательной в этой точке.

Обозначим наклоны касательных в двух концах через — θ и θ + , напряжения — через Т и T + dT и линейный вес[4] нити — через т. Тогда, если три силы разложены на их х- и y- компоненты, мы получим соответственно:

Если элемент нити должен быть в равновесии, под действием этих сил необходимо, чтобы сумма компонент X и сумма компонент У были ну лями, т. е.:

Деля почленно эти уравнения, имеем:

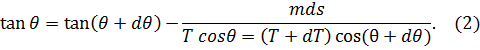
Первое из уравнений (1) утверждает, что горизонтальная компонента натяжения одна и та же в двух концах элемента ds.

Так как элемент ds произвольно выбранный, то отсюда следует, что эта компонента одна и та же в каждой точке кривой[5]. Если обозначим ее через k, то (2) примет вид:

Если мы запишем это последнее в виде

и будем приближать ds и dθ к нулю, то левая часть уравнения обратится в производную tan θ. Итак:

Это и есть дифференциальное уравнение искомой кривой, выраженное, как говорят математики, во внутренней форме, т. е. оно выражает длину s, измеренную, начиная с некоторой точки, в функции наклона касательной. Для многих вопросов, однако, внутренняя форма не очень удобна, и поэтому лучше свести ее к обычной декартовой форме. Для этого нужно произвести замену обеих переменных s и θ на х и у, связанных с первыми соотношениями:

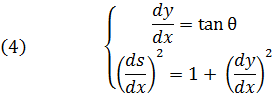
Переменное s исключается, если мы заметим, что

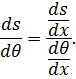
Это дает

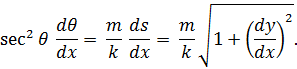
Дифференцируя первое из уравнении (4) по х, мы получаем:

Результат подстановки будет поэтому:

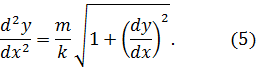
Упростив (5), получаем:

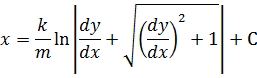
Это и есть дифференциальное уравнение кривой провеса нити, выраженное в функции декартовых координат х и у.

Поверхность вращения наименьшей площади

Если две точки А и В (см. рисунок) связаны кривой y = f(x) и вся эта фигура вращается около оси x, то кривая образует при этом поверхность вращения.

Площадь этой поверхности зависит от формы кривой, т. е. от формы функции f(x). Существует кривая, обладающая тем свойством, что ее поверхность вращения имеет наименьшую площадь.

Задача состоит в том, чтобы найти уравнение этой кривой. Так как задача похожа на те задачи анализа, где приходится отыскивать точки максимума или минимума кривой, то полезно напомнить рассуждение, при помощи которого такие задачи решаются. Оно состоит в основном из трех шагов.

1) Абсцисса минимальной точки предполагается сначала известной и обозначается, например, буквой х.

2) Отмечается, что передвижение из точки минимума в любом направлении увеличивает функцию, другими словами, что f(x+ε) и f(xε) больше f(x).

3) Если ε очень мало, то

f(x+ε) f(x)+εf(x — r)f(x) ε.

Одно из этих выражений больше f(x), а другое меньше, если только f (х) не обращается в нуль. Но в силу 2) этого быть не может, следовательно в точке минимума производная функция должна исчезать.

Конечно, этого одного недостаточно. Напомним, что условие 3) необходимо также для максимума, и до тех пор пока мы не рассмотрели вторую произ-водную, нельзя узнать, что именно мы получили.

Однако это все, что нужно для наших целей.

Мы решим нашу задачу путем совершенно аналогичным.

1) Предполагаем, что искомая кривая известна и что ее уравнение есть

y=f(x).

2) Если будем менять форму кривой произвольно, то площадь поверхности вращения должна при этом увеличиваться. Если обозначить разность между ординатами новой и старой кривых через ε(x), то новое уравнение будет:

y = f(x) + ε(x).

3) Можно показать, что если некоторое дифференциальное выражение не равно нулю, то площадь, описанная кривой f(х)+ε(х), будет больше площади, описанной кривой f(x), а площадь, описанная кривой f(х) ε(x), будет меньше этой последней. Отсюда дифференциальное выражение должно исчезать. Это приводит к дифференциальному уравнению, решение которого определяет искомую кривую.

После того как мы наметили таким образом нашу задачу, приступим к детальному проведению третьего шага. Прежде всего нужна написать выражение для площади поверхности вращения. Это- простая задача анализа, ответом на которую служит выражение:

 Скачать реферат