Целочисленные функции
2 случай: если ![]() , то
, то ![]() , так как f – убывающая функция;
, так как f – убывающая функция; ![]() (в силу того, что функция «пол» — неубывающая).
(в силу того, что функция «пол» — неубывающая).
Если ![]() , то существует такое чи
, то существует такое чи
сло ![]() , что
, что ![]() и
и ![]() (так как f непрерывна). Поскольку f(y) целое, то по условию
(так как f непрерывна). Поскольку f(y) целое, то по условию ![]() целое. А это противоречит тому, что между x и éxù не может быть никакого целого числа. Следовательно,
целое. А это противоречит тому, что между x и éxù не может быть никакого целого числа. Следовательно, ![]() .
.
Что и требовалось доказать.
Задача 6.
Решите рекуррентность при целом ![]()
![]() при
при ![]() ,
,
![]() при
при ![]() .
.
Решение:
Покажем, что 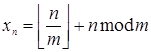 методом математической индукции по
методом математической индукции по ![]() .
.
База: ![]() : из того, что
: из того, что ![]() , следует, что
, следует, что ![]() , тогда
, тогда 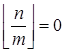 и
и ![]() , поэтому для
, поэтому для ![]() выполняется
выполняется 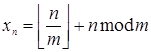 .
.
Переход: пусть для некоторого номера ![]() и для меньших номеров утверждение верно:
и для меньших номеров утверждение верно: 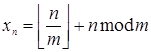 .
.
Докажем, что 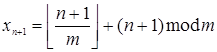 .
.
![]() =
=![]()
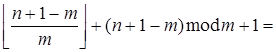
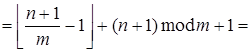
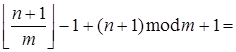
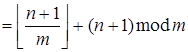 .
.
Что и требовалось доказать.
Задача 7.
Докажите принцип ящиков Дирихле: если n предметов размещены по m ящикам, то некоторый ящик должен содержать не меньше чем én/mù предметов, а некоторый ящик должен содержать не более чем ën/mû.
Решение:
Предположим, что каждый ящик содержит меньше, чем én/mù предметов. Тогда наибольшее количество предметов в каждом ящике — это 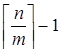 предметов. Следовательно, наибольшее количество предметов, размещённых по ящикам — это
предметов. Следовательно, наибольшее количество предметов, размещённых по ящикам — это ![]() Þ
Þ ![]() Þ
Þ ![]() . Это противоречит тому, что
. Это противоречит тому, что ![]() .
.
Значит, существует ящик, который содержит не менее чем én/mù предметов.
Предположим, что нет ящика, в котором не более, чем ën/mû предметов, т.е. каждый ящик содержит более чем ën/mû предметов. Тогда наименьшее количество предметов в каждом ящике — ![]() . Следовательно, наименьшее количество предметов, размещённых по ящикам — это
. Следовательно, наименьшее количество предметов, размещённых по ящикам — это ![]() Þ
Þ ![]() Þ
Þ ![]() . Это противоречит тому, что
. Это противоречит тому, что ![]() .
.
Значит, существует ящик, который содержит не более чем ën/mû предметов.
Что и требовалось доказать.
Задача 8.
Покажите, что выражение ![]() всегда равно либо ëxû, либо éxù. При каких условиях получается тот или иной случай?
всегда равно либо ëxû, либо éxù. При каких условиях получается тот или иной случай?
Решение:
1 случай: x = (4k-1)/2, kÎZ
Тогда ![]() , так как
, так как ![]() - целое число.
- целое число.
Получим ![]() =
=![]() =
=![]() =
=![]() =
=![]()
2 случай: x ¹ (4k-1)/2, k Î Z, тогда ![]() .
.
Получим ![]() =
=![]() =
=![]()
Итак, данное выражение округляет числа до ближайшего целого; в случае «равновесия» — когда x лежит ровно посередине между целыми числами — данное выражение округляет число в сторону чётного.
Задача 9.
Докажите, что ![]() при любом целом n и любом целом положительном m.
при любом целом n и любом целом положительном m.
Доказательство:
Пусть 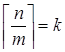 .
.
Покажем, что 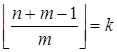 .
.
Имеем 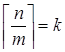 Û
Û
Û ![]() (по свойствам (4)) Û
(по свойствам (4)) Û
Û ![]() Û
Û
Û ![]() Û
Û
Û ![]() Û
Û
Û ![]() Û
Û
Û 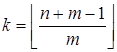
Что и требовалось доказать.
Задача 10.
Пусть α и β — вещественные положительные числа. Докажите, что Spec(α) и Spec(β) образуют разбиение всех целых положительных чисел тогда и только тогда, когда α и β иррациональны и 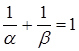 .
.
Другие рефераты на тему «Математика»:
Поиск рефератов
Последние рефераты раздела
- Анализ надёжности и резервирование технической системы
- Алгоритм решения Диофантовых уравнений
- Алгебраическое доказательство теоремы Пифагора
- Алгоритм муравья
- Векторная алгебра и аналитическая геометрия
- Зарождение и создание теории действительного числа
- Вероятностные процессы и математическая статистика в автоматизированных системах
