Целочисленные функции

Следовательно, равенство верно для любого натурального n. Что и требовалось доказать.

Найдём аналогичное выражение для , т.е. найдём коэффициенты a, b, c.

Поскольку — есть корень третьей степ

ени из 1, то и .

Так как , то .

При делении числа на 3 возможны только три различных остатка: либо 0, либо 1, либо 2.

Если , то .

Если , то .

Если , то .

Решая систему 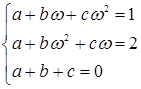, находим a, b, c.

, , .

Итак, получаем следующую формулу:

.

Задача 14.

Какому необходимому и достаточному условию должно удовлетворять вещественное число , чтобы равенство выполнялось при любом вещественном ?

Решение:

При любом вещественном и равенство выполняется Û b — целое число.

Если b — целое число, то функция непрерывная, возрастающая функция (так как ). Пусть — целое число, т.е. . Тогда , так как и . Выражая через , получим — целое, как натуральное число в неотрицательной целой степени. Поэтому можно применить формулу (6) и получить равенство .

Если b — не целое число, то при равенство не будет выполняться, так как

Итак, если , то равенство выполняется при любом вещественном тогда и только тогда, когда b — целое число.

Ответ: b — целое число.

Задача 15.

Найдите сумму всех чисел, кратных x, в замкнутом интервале [a, b], при .

Решение:

Числа, кратные имеют вид , где . Нужно просуммировать те из чисел , для которых . Учитывая, что и (4), имеем

Û Û .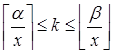

Нам нужно вычислить следующую сумму:

.

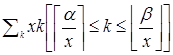В этой сумме можно вынести за скобки, а в скобке останется сумма всех чисел от до включительно. Применяя формулу арифметической прогрессии получаем:

.

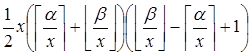Задача 16.

Покажите, что n-й член последовательности 1,2,2,3,3,3,4,4,4,4,5,5,5,5,5,… равен. (Каждое число m входит в данную последовательность m раз.)

Решение:

В этой последовательности чисел меньших будет , а чисел не превосходящих будет . Поэтому, если xn=m, то

Оценим n:

Û

Û Û

Û Û

Û 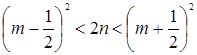Û

Û Û

Û Û

Û Þ

Þ .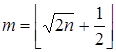

Следовательно, .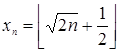

Задача 17.

Найдите и докажите связь между мультимножествами Spec(α) и Spec(α/(α+1)), где α — некоторое положительное вещественное число.

 Скачать реферат