Методы отсечения

– целые, (42)

Ранг матрицы считаем равным m.

Теорема. Пусть x(£r, C)=xr является оптимальным опорным планом задачи (£r, C) и xr не удовлетворяет условию целочисленности, Nr

– множество индексов, нумерующих небазисные переменные, соответствующие xr.

Тогда неравенство

(43)

является правильным отсечением.

Правильное отсечение, отсекающее нецелочисленный оптимум x(£r, C) задачи (£r, C), можно записать следующим образом:

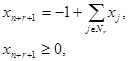
– целое.

Заметим, что каждая из вновь вводимых переменных однозначно определяется заданием переменных , так что .

Обозначим через упорядоченные в порядке возрастания компоненты плана x задачи (39) – (41), так что

(44)

Положим

(45)

Лемма. Если для некоторого плана x задачи (39) – (41)

, (46)

то

(47)

Доказательство проведем по индукции. Сначала докажем, что

(47¢)

По определению

(48)

Так как ранг матрицы равен m, то

где – число элементов множества . Из определения чисел получаем

(49)

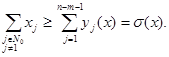(50)

Из (48), (49), (50) и (46) имеем

Лемма доказана при р=1.

Теперь допустим, что лемма верна при , и докажем ее при :

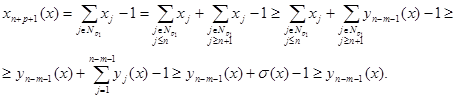
Лемма доказана.

Пользуясь леммой, докажем две теоремы.

Теорема 1. Если каждый оптимальный план задачи (39) – (42) содержит не менее (m+2) положительных компонент, то алгоритм Данцига не будет конечным.

Доказательство. Допустим, что на s-й итерации алгоритма Данцига получится искомый оптимальный план . Рассмотрим числа

(51)

Все они целые и среди них должно быть (n-m) нулей – это небазисные переменные . Кроме того, по условию среди чисел , должно быть по крайней мере (m+2) положительных числа, т.е. не больше чем (n-m-2) нулей.

По определению чисел отсюда следует, что

а так как должно быть целым, то

(52)

Но по определению чисел

(53)

Из (52) получаем

(54)

и по лемме

(55)

Из (52), (53) и (55) следует, что среди чисел (51) по крайней мере [1+(m+1)+s] = [m+2+s] положительных, а следовательно, не больше чем [n+s – (m+2+s)] = (n-m-2) нулей. Но выше было отмечено, что среди чисел (51) должно быть (n-m) нулей. Получилось противоречие. Теорема 1 доказана.

Следствие (из теоремы 1). Для того чтобы алгоритм Данцига был конечным, необходимо, чтобы искомый оптимальный план лежал на ребре многогранного множества (40) – (41) (предполагается, что задача (39) – (41) невырожденная).

Хотя это условие и является весьма жестким, ему удовлетворяют, например, все (невырожденные) задачи следующего вида.

Максимизировать

(56)

при условиях

(57)

(58)

(59)

– целое, (60)

А это важный класс задач.

Однако приведенное в следствии необходимое условие конечности алгоритма Данцига не является достаточным. Действительно, имеет место следующая

Теорема 2. Если для некоторого оптимального плана x' задачи (39) – (42) и некоторого плана x» задачи (39) – (41) имеют место неравенства

(61)

и

(62)

то алгоритм Данцига не будет конечным.

Доказательство. Допустим, что алгоритм Данцига конечен. Тогда из (61) следует, что точка x» была отсечена на некоторой (скажем, р-й) итерации, так что

(63)

Но из (62) и леммы получим

(64)

Сравнивая (63) и (64), получаем противоречие. Теорема 2 доказана.

Итак, упрощенный алгоритм Данцига будет конечным лишь в весьма редких случаях.

7. Некоторые выводы

Попробуем охарактеризовать поведение алгоритмов метода отсечения при решении задач целочисленного линейного программирования. В качестве меры продолжительности вычислений могут рассматриваться количество симплексных итераций I и количество правильных отсечений (дополнительных линейных ограничений) D.

 Скачать реферат