Методы отсечения

Рефераты / Математика / Методы отсечения

Теорема. Пусть x(£k, C) – оптимальное решение задачи (27–28, 30), – элементы симплексной таблицы, соответствующей ему.

Если x(£k, C) является недопустимым решением задачи (27–30) и , тогда, используя i-ю строку симплексной таблицы, можно постр

оить отсечение, обладающее свойством правильности по формулам:

(31)

(32)

где

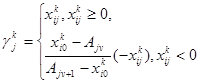(33)

Доказательство. Проверим вначале условие отсечения. Пусть в оптимальном решении x(£k, C) координата не удовлетворяет условию (29). Покажем, что в этом случае вектор х(£k, C) не удовлетворяет условиям (31, 32). Поскольку Nk – множество индексов небазисных переменных xi, которые в оптимальном решении равны нулю, то равенство (31) принимает вид и будет отрицательным согласно условию теоремы. Следовательно, , т.е. условие отсечения не выполняется.

Проверим условие правильности. Для этого покажем, что любое допустимое решение задачи (27–30) удовлетворяет условиям (31, 32).

Запишем разложение для координаты допустимого решения задачи (27–30) по небазисным переменным

(34)

и рассмотрим два случая: a) ; б) . Введем обозначения:

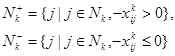
и представим (34) в виде

где

Очевидно, так как .

Рассмотрим случай а): , или что все равно, .

Отсюда Но поэтому

(35)

Домножим обе части (35) на неотрицательную величину и сложим с неотрицательной величиной :

(36)

Рассмотрим случай б): или, что все равно, Так как по определению , то Умножим обе части неравенства на неотрицательную величину и на -1, получим . Прибавляя к полученному выражению неравенство , получим

(37)

Таким образом, в а) и в б) случаях пришли к одному и тому же неравенству (36) и (37). Пользуясь ранее введенными обозначениями, их можно записать

(38)

Формула (38) определяет правильные отсечения. Сравнивая ее с выражением (31–32), приходим к выводу, что коэффициенты определяются следующим образом:

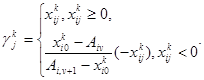
Теорема доказана.

Алгоритм Дальтона – Ллевелина может быть описан следующим образом.

1. Решается (£k, C) – задача (27–30) (вначале k = 0). Пусть x(£k, C), k = 0, 1, 2,… оптимальное решение (£k, C) – задачи, – симплексная таблица.

2. Проверяется условие допустимости по всем координатам оптимального вектора решения х(£k, C) (£k, C) – задачи. Если условие допустимости выполняется, то полученное решение является оптимальным решением исходной задачи (27–30). Если условие допустимости не выполняется хотя бы по одной координате, осуществляется переход к 3.

3. Пусть не удовлетворяет условию допустимости. Тогда выбирается

i0 = min {i| 1<i<n1, хj0k – не удовлетворяет (29)}.

4. Для выбранного номера i=i0 строится правильное отсечение, т.е. вводится дополнительная переменная

где определяется формулой (33),

5. Добавляем линейное ограничение, определяющее правильное отсечение, к условиям (£k, C) – задачи и получаем новую (£k+1, C) – задачу. Полагая k = k + 1, переходим к п. 1.

Приведем без доказательства теорему о конечности алгоритма.

Теорема. Если: коэффициенты целевой функции дискретны; F(x) ограничена снизу на многогранном множестве £; задача (£, C) имеет по крайней мере одно решение; выбор строки для построения правильного отсечения производится по правилу минимального номера и (£k, C) – задачи решаются методом последовательного уточнения оценок, то алгоритм Дальтона и Ллевелина сходится.

6. Алгоритм Данцига

Способ построения правильных отсекающих плоскостей, предложенный Данцигом значительно проще, чем все изложенные выше способы. Но, как показали Гомори и Гофман, конечность алгоритма Данцига гарантируется лишь для очень узкого класса задач. На примере алгоритма Данцига видно, насколько тонким является вопрос о построении правильных отсечений и сколь осторожно следует подходить к различным упрощенным алгоритмам.

Рассматривается полностью целочисленная задача линейного программирования:

Максимизировать

(39)