Методы отсечения

Рефераты / Математика / Методы отсечения

Обозначим через k номер псевдорешения (£k, C) – задачи; тогда направляющей строкой является i+k+1-я строка, k =0, 1, 2,…. Поэтому на каждом этапе преобразования таблицы вектор Ai+k+i будет выводиться из таблицы. Можно доказать, что через конечное число шагов либо будет найдено целочисленное решение, либо будет обнаружена ее неразрешимость, а тем самым неразрешимость (£ц, C) – задачи

Если решение (£k, C) – задачи завершается построением оптимального целочисленного решения x*, то m, первых его компонент определяют решение целочисленной задачи; если среди координат х* есть дробные, то одна из дробных компонент (ранее определенным правилом) порождает дополнительное ограничение и процесс решения должен быть продолжен с новой окаймляющей строкой. Строка, используемая ранее для окаймления, вычеркивается и больше для построения расширенных задач не восстанавливается.

Процедуру решения (£k, C) – задачи (k=0, 1,…) и анализа полученного решения назовем большой итерацией. Номер большой итерации совпадает с номером решаемой (£k, C) – задачи.

Результатом большой итерации является переход к новой (£k+1, C) – задаче либо окончание решения задачи.

Сделаем некоторые пояснения к блок-схеме алгоритма.

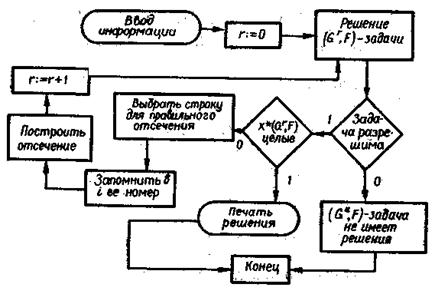
Введем: 1) ячейку i, в которой будем запоминать номер строки, на основании которой строится очередное дополнительное линейное ограничение, 2) счетчик r, соответствующий номеру проводимой большой итерации. Обозначим x*(£r, C) оптимальное решение (£r, C) – задачи. Заметим, что обозначение (£r, C) – задача, эквивалентное (£r, C), введено в блок-схеме для удобства записи.

При некоторых условиях удается доказать теорему о конечности первого алгоритма Гомори, которую мы приведем без доказательства.

Теорема. Пусть множество оптимальных планов задачи (£0, C) ограничено и выполняются следующие условия:

1) сi – целые коэффициенты целевой функции F(x) (i =1,2,…, n), строка целевой функции в симплексной таблице учитывается при выборе строки для построения правильного отсечения;

2) справедливо одно из двух утверждений: либо целевая функция ограничена снизу на Сo, либо задача (£ц, C) имеет хотя бы один план х'.

Тогда первый алгоритм Гомори требует конечного числа больших итераций.

4. Второй алгоритм Гомори

Второй алгоритм Р. Гомори предназначается для решения задач, в которых требование целочисленности наложено на некоторые переменные (в частности и на все). Мы его рассмотрим применительно к задачам частично целочисленного типа, понимая, что вычислительная схема будет справедливой и для задач, полностью целочисленных.

Пусть в области, определенной условиями:

(20)

(21)

– целые, (22)

требуется максимизировать функцию

(23)

Метод решения задачи (20–23) основывается на той же идее, что и метод решения полностью целочисленных задач. А именно: строится область £k, которая при k = 0 определяется условиями (20–21); решается полученная при этом задача линейного программирования (20–21, 23). Если задача (20–21, 23) оказывается разрешимой, то полученное оптимальное решение ее анализируется на допустимость для исходной задачи целочисленного программирования (20–23). Если найденное решение оказывается целочисленным, то одновременно оно будет оптимальным для (20–23). Если оптимальное решение (£k, C) – задачи оказывается недопустимым для исходной задачи (20–23), то осуществляется построение правильного отсечения и переход к решению новой задачи,

Второй алгоритм Р. Гомори формулируется в виде следующей теоремы:

Теорема. Пусть х(£k, C) – оптимальное решение (£k, C) – задачи, – элементы соответствующей ему симплексной таблицы. Если – нецелое , то

(24)

– целое, (25)

где

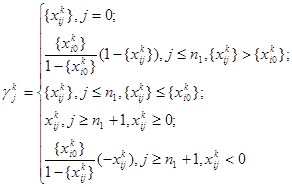(26)

определяет правильное отсечение. Блок-схема второго алгоритма Р. Гомори аналогична блок-схеме первого алгоритма Р. Гомори и отличается лишь правилом построения коэффициентов правильного отсечения.

Правило построения правильного отсечения

Пусть x(£k, C) не удовлетворяет условию целочисленности, – элементы симплексной таблицы, соответствующей полученному оптимальному решению (£k, C) – задачи. Выберем i0=min {i | i Î (1, 2,…, n), xi0k – нецелое} и строим правильное отсечение по формулам (24 – 26).

Условия конечности второго алгоритма Гомори:

1) Целевая функция F(x) удовлетворяет условию целочисленности. Это учитывается при выборе строки k для построения правильного отсечения.

2) Выполнено по крайней мере одно из двух условий:

2') целевая функция ограничена снизу на многогранном множестве £= £0;

2») задача (£0ц, C) имеет по крайней мере один план.

С помощью второго алгоритма Гомори можно (в случае n1=n) решать и полностью целочисленную задачу линейного программирования. Однако в этом случае нет оснований для сравнения эффективности второго и первого алгоритмов Гомори.

5. Алгоритм Дальтона и Ллевелина

Второй алгоритм Гомори имеет дело с частично целочисленными задачами линейного программирования. Дальтон и Ллевелин рассматривают 0 олее широкий класс задач – частично дискретные задачи линейного программирования и применительно к ним модифицируют второй алгоритм Гомори.

Напомним, что решением задачи дискретного программирования будем называть вектор, координаты которого принадлежат £ц области вида:

(27)