Предельные точки
Если ![]() и
и ![]() эквивалентны, то говорят, что они имеют одинаковую мощность.
эквивалентны, то говорят, что они имеют одинаковую мощность.
Можно привести важный пример эквивалентности бесконечных множеств.
Утверждение 1: Множество Доказательство: достаточно показать, как присвоить собственный номер каждому рациональному числу. Для этого представим каждое рациональное число в виде несократимой дроби:
Такое представление единственно. Высотой рационального числа Будем нумеровать дроби в порядке возрастания и т.д. Ясно, что каждое рациональное число когда-нибудь получит свой порядковый номер. При этом все номера 1,2,3,… будут использованы и разные рациональные числа получат разные номера. Тем самым построено взаимно однозначное соответствие множеств Всякое множество, эквивалентное множеству натуральных чисел, называется счетным множеством.
Исходя из этого определения, можно упомянуть о некоторых теоремах:
1. Из всякого бесконечного множества можно выделить счетное подмножество.
2. Всякое бесконечное подмножество счетного множества тоже счетно.
3. Сумма конечного числа счетных множеств – тоже счетное множество.
4. Сумма счетного множества счетных множеств – тоже счетное множество.
5. Сумма конечного или счетного множества множеств, каждое из которых конечно или счетно, есть конечное или счетное множество.
6. Множество всех рациональных чисел счетно.
7. Множество Утверждение 2. Всякое непустое подмножество счетного множества конечно или счетно.
Доказательство: занумеруем элементы счетного множества и перенумеруем затем элементы подмножества в порядке возрастания этих номеров. Если мы исчерпаем все подмножество на конечном шаге, то оно конечно, иначе - счетно.
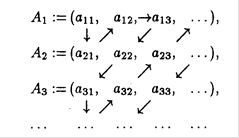
Утверждение 3. Сумма конечного или счетного числа счетных множеств счетна.
Доказательство. Проведем нумерацию элементов суммы множеств по схеме:
За Стоит обратить внимание, что бесконечные множества, рассмотренные в утверждениях 1-3, оказались равномощными, точнее счетными. Но не все бесконечные множества равномощны. Имеет место следующая теорема.
Теорема 1: совокупность Доказательство: (от противного). Пусть ![]() (натуральных чисел) и множество
(натуральных чисел) и множество ![]() ) эквивалентны.
) эквивалентны.
![]()
![]() назовем величину
назовем величину ![]() . Эта высота сама является натуральным числом, т.е. принимает значения 1,2,3,… и т.д. При фиксированном
. Эта высота сама является натуральным числом, т.е. принимает значения 1,2,3,… и т.д. При фиксированном ![]() существует не более
существует не более ![]() различных несократимых дробей, т.к. тогда знаменатель
различных несократимых дробей, т.к. тогда знаменатель ![]() может принимать значения 1,2,…,
может принимать значения 1,2,…,![]() , а для данного
, а для данного ![]() числитель
числитель ![]() числа
числа ![]() может принимать не более двух значений:
может принимать не более двух значений: ![]() . Таким образом, с данной высотой
. Таким образом, с данной высотой ![]() число рациональных чисел не более
число рациональных чисел не более ![]() .
.
![]() ; при фиксированном
; при фиксированном ![]() в порядке возрастания
в порядке возрастания ![]() , а при фиксированных
, а при фиксированных ![]() и
и ![]() - в порядке возрастания
- в порядке возрастания ![]() . Тогда получим:
. Тогда получим:
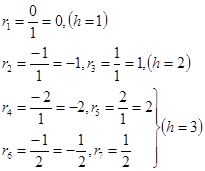
![]() и
и ![]() .
.
![]() всех алгебраических полиномов с рациональными коэффициентами счетно.
всех алгебраических полиномов с рациональными коэффициентами счетно.
![]() шагов будут заведомо занумерованы все элементы
шагов будут заведомо занумерованы все элементы ![]() .
.
![]() всех подмножеств любого множества X сама образует множество, не эквивалентное X. Эта теорема (точнее, ее модификация
всех подмножеств любого множества X сама образует множество, не эквивалентное X. Эта теорема (точнее, ее модификация ![]() ~
~![]() ) была доказана Г. Кантором (1845-1918) в 1874 г.
) была доказана Г. Кантором (1845-1918) в 1874 г.
![]() ~
~![]() . Значит имеется биективное соответствие
. Значит имеется биективное соответствие ![]() Тогда, если
Тогда, если ![]() , то ему однозначно соответствует
, то ему однозначно соответствует ![]() . Теперь всякую точку
. Теперь всякую точку ![]() назовем правильной, если она принадлежит своему образу, т.е., если
назовем правильной, если она принадлежит своему образу, т.е., если ![]() . В противном случае эту точку
. В противном случае эту точку ![]() будем называть особой точкой. Назовем дефектом множество
будем называть особой точкой. Назовем дефектом множество ![]() , состоящее из всех особых точек
, состоящее из всех особых точек ![]() . Тогда ясно, что
. Тогда ясно, что ![]() является элементом множества
является элементом множества ![]() . В силу наличия взаимно однозначного соответствия
. В силу наличия взаимно однозначного соответствия ![]() между
между ![]() и
и ![]() найдется такая точка
найдется такая точка ![]() . При этом сама точка
. При этом сама точка ![]() обязана быть либо правильной, либо особой. Но первое не имеет места, поскольку тогда бы по определению правильной точки она принадлежала бы
обязана быть либо правильной, либо особой. Но первое не имеет места, поскольку тогда бы по определению правильной точки она принадлежала бы ![]() , что невозможно, т. к. ко множеству
, что невозможно, т. к. ко множеству ![]() по построению отнесены только особые точки. Но второй случай приводит к противоречию, т. к. тогда по определению особой точки
по построению отнесены только особые точки. Но второй случай приводит к противоречию, т. к. тогда по определению особой точки ![]() , а с другой стороны, тогда точка
, а с другой стороны, тогда точка ![]() как особая точка должна войти в дефект
как особая точка должна войти в дефект ![]() по его построению.
по его построению.
Другие рефераты на тему «Математика»:
Поиск рефератов
Последние рефераты раздела
