Решение дифференциальных уравнений
в) ![]() ; г)
; г) ![]() .
.
5. f(x) =1- x, g(x) = 3 - 2x - x2.
6. ![]() .
.
7. 9. 10. Вариант 4
1. а) в) д) 2. а) в) 3. а) 4. а) в) 5. f(x) = x, g(x) = 2 + 2x - x2.
6. 7. 8. 9. 10. Вариант 5
1. а) в) д) 2. а) в) 3. а) 4. а) в) 5. f(x) = x2 - x + 1, g(x) = x + 1.
6. 7. 8. 9. 10. Вариант 6
1. а) в) д) 2. а) в) 3. а) 4. а) в) 5. f(x) = 2 - 2x2, g(x) = x+1.
6. 7. 8. 9. 10.
Вариант 7
1. а) в) д) 2. а) в) 3. а) ![]()
![]() .
.
![]() ;
; ![]()
![]()
![]() .
.
![]() .
.
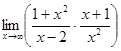 ; б)
; б) 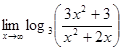 ;
;
![]() ; г)
; г) ![]() ;
;
![]() ; е)
; е) ![]() .
.
![]() ; б)
; б) ![]() ;
;
![]() ; г)
; г) ![]() ;
;
![]() ; б)
; б) ![]() ;
;
![]() ; б)
; б) ![]() ;
;
![]() ; г)
; г) ![]() .
.
![]() .
.
![]()
![]() .
.
![]() ;
; ![]()
![]()
![]() .
.
![]() .
.
![]() ; б)
; б) ![]() ;
;
![]() ; г)
; г) ![]() ;
;
![]() ; е)
; е) ![]() .
.
![]() ; б)
; б) 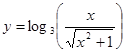 ;
;
![]() ; г)
; г) ![]() ;
;
![]() ; б)
; б) ![]() ;
;
![]() ; б)
; б) ![]() ;
;
![]() ; г)
; г) ![]() .
.
![]() .
.
![]()
![]() .
.
![]() ;
; ![]()
![]()
![]() .
.
![]() .
.
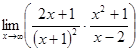 ; б)
; б) 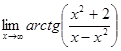 ;
;
![]() ; г)
; г) ![]() ;
;
![]() ; е)
; е) ![]() .
.
![]() ; б)
; б) ![]() ;
;
![]() ; г)
; г) ![]() ;
;
![]() ; б)
; б) ![]() ;
;
![]() ; б)
; б)![]() ;
;
![]() ; г)
; г) ![]() .
.
![]() .
.
![]()
![]() .
.
![]() ;
; ![]()
![]()
![]() .
.
![]() .
.
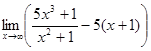 ; б)
; б) ![]() ;
;
![]() ; г)
; г) ![]() ;
;
![]() ; е)
; е) ![]() .
.
![]() ; б)
; б) ![]() ;
;
![]() ; г)
; г) ![]() ;
;
![]() ; б)
; б) ![]() ;
;
Другие рефераты на тему «Математика»:
Поиск рефератов
Последние рефераты раздела
