Методы решения уравнений линейной регрессии

Задача

По предприятиям легкой промышленности региона получена информация, характеризующая зависимость объема выпуска продукции (Y, млн.руб.) от объема капиталовложений (Х, млн.руб.)

Требуется:

1. Найти параметры уравнения линейной регрессии, дать экономическую интерпретацию коэффициента регрессии.

2. Вычислить остатки; найти остаточную сумму квадратов; оценить дисперсию остатков ; построить график остатков.

3. Проверить выполнение предпосылок МНК.

4. Осуществить проверку значимости параметров уравнения регрессии с помощью t-критерия Стьюдента (α=0,05).

5. Вычислить коэффициент детерминации, проверить значимость уравнения регрессии с помощью F-критерия Фишера (α=0,05), найти среднюю относительную ошибку аппроксимации. Сделать вывод о качестве.

6. Осуществить прогнозирование среднего значения показателя Y при уровне значимости α=0,01 при Х=80% от его максимального значения.

7. Представить графически фактических и модельных значений Y, точки прогноза.

8. Составить уравнения нелинейной регрессии:

· Гиперболической;

· Степенной;

· Показательной.

Привести графики построенных уравнений регрессии.

9. Для указанных моделей найти коэффициенты детерминации, коэффициенты эластичности и средние относительные ошибки аппроксимации. Сравнить модели по этим характеристикам и сделать вывод.

Решение

1. Уравнение линейной регрессии имеет вид:

= а0 + а1x.

Построим линейную модель.

Для удобства выполнения расчетов предварительно упорядочим всю таблицу исходных данных по возрастанию факторной переменной Х (Данные => Сортировка). ( рис. 1).

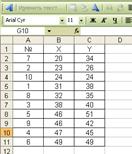
Рис.1

Используем программу РЕГРЕССИЯ и найдем коэффициенты модели (рис.2)

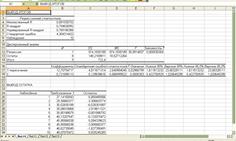
Рис.2

Коэффициенты модели содержатся в таблице 3 (столбец Коэффициенты).

Таким образом, модель построена и ее уравнение имеет вид

Yт = 12,70755+0,721698Х.

Коэффициент регрессии b=0,721698, следовательно, при увеличении объема капиталовложений (Х) на 1 млн руб. объем выпуска продукции (Y) увеличивается в среднем на 0,721698 млн руб.

2. Вычислить остатки; найти остаточную сумму квадратов; оценить дисперсию остатков S²e; построить график остатков.

Остатки содержатся в столбце Остатки итогов программы РЕГРЕССИЯ (таблица 4).

Программой РЕГРЕССИЯ найдены также остаточная сумма квадратов SSост=148,217 и дисперсия остатков MS=18,52712 (таблица 2).

Для построения графика остатков нужно выполнить следующие действия:

· Вызвать Матер Диаграмм, выбрать тип диаграммы Точечная (с соединенными точками).

· Для указания данных для построения диаграммы зайти во вкладку Ряд, нажать кнопку Добавить; в качестве значений Х указать исходные данные Х (таблица 1);значения Y - остатки (таблица 4).

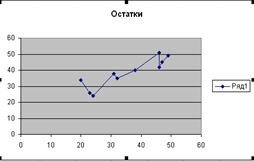
Рис.3 График остатков

3. Проверить выполнение предпосылок МНК.

Предпосылками построения классической линейной регрессионной модели являются четыре условия, известные как условия Гаусса-Маркова.

· В уравнении линейной модели Y=a+b*X+ε слагаемое ε - случайная величина, которая выражает случайный характер результирующей переменной Y.

· Математическое ожидание случайного члена в любом наблюдении равно нулю, а дисперсия постоянна.

· Случайные члены для любых двух разных наблюдений независимы (некоррелированы).

· Распределение случайного члена является нормальными.

1) Проведем проверку случайности остаточной компоненты по критерию повторных точек.

Количество повторных точек определим по графику остатков: p=5

Вычислим критическое значение по формуле:

.

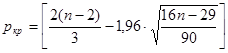При найдем

Схема критерия:

Сравним , следовательно, свойство случайности для ряда остатков выполняется.

1. Равенство нулю математического ожидания остаточной компоненты для линейной модели, коэффициенты которой определены по МНК, выполняется автоматически. С помощью функции СРЗНАЧ для ряда остатков можно проверить: .

Свойство постоянства дисперсии остаточной компоненты проверим по критерию Гольдфельда–Квандта.

В упорядоченных по возрастанию переменной X исходных данных () выделим первые 4 и последние 4 уровня, средние 2 уровня не рассматриваем.

С помощью программы РЕГРЕССИЯ построим модель по первым четырем наблюдениям (регрессия-1), для этой модели остаточная сумма квадратов .

 Скачать реферат