Основные понятия и методы экономико-математического моделирования
![]() ,
,
k – количество дополнительных переменных,и условие неотрицательности искомых переменных:
![]() .
.
В результате решения задачи находится некий план (программа) работы некоторого предприятия. Отсюда и появилось слово «программирование». Слово
линейное указывает на линейный характер зависимости как в целевой функции, так и в системе ограничений. Следует еще раз подчеркнуть, что задача обязательно носит экстремальный характер, т.е. состоит в отыскании максимума или минимума (экстремума) целевой функции.
Геометрическая интерпретация оптимизационных задач линейного программирования.
Пусть необходимо найти оптимальный план производства двух видов продукции (x1 и x2), т.е. такой план, при котором целевая функция (общая прибыль) была бы максимальной, а имеющиеся ресурсы использовались бы наилучшим образом. Условия задачи приведены в таблице:
| Вид продукции | Норма расхода ресурса на единицу продукции | Прибыль на единицу изделия | ||
| А | В | С | ||
| 1 | 2 | 0,1 | 3,5 | 4 |
| 2 | 1 | 0,5 | 1 | 5 |
| Объем ресурса | 12 | 4 | 18 | |
Оптимизационная модель задачи запишется следующим образом:
а) целевая функция:
![]()
б) ограничения:
2х1 + х2 ![]() 12 (ограничение по ресурсу А);
12 (ограничение по ресурсу А);
0,1х1 + 0,5х2 ![]() 4 (ограничение по ресурсу B);
4 (ограничение по ресурсу B);
3,5х1 + х2 ![]() 18 (ограничение по ресурсу C).
18 (ограничение по ресурсу C).
в) условие неотрицательности переменных:
![]()
Данную и подобные оптимизационные модели можно продемонстрировать графически (Рис.3.3.).
Преобразуем нашу систему ограничений, найдя в каждом из уравнений x2 , и отложим их на графике. Любая точка на данном графике с координатами x1 иx2 представляет вариант искомого плана. Однако ограничение по ресурсу А сужает область допустимых решений. Ими могут быть все точки, ограниченные осями координат и прямой АА, т.к. не может быть израсходовано ресурса А больше, чем его на предприятии имеется. Если точки находятся на самой прямой, то ресурс используется полностью.
Аналогичные рассуждения можно привести и для ресурсов В и С. В результате условиям задачи будет удовлетворять любая точка, лежащая в пределах заштрихованного многоугольника. Данный многоугольник называется областью допустимых решений.

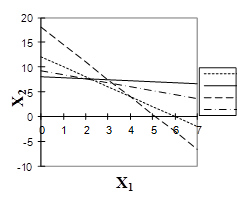
Рис. 3.3. Геометрическая интерпретация оптимизационной задачи линейного программирования
Однако нам необходимо найти такую точку, в которой достигался бы максимум целевой функции. Для этого построим произвольную прямую 4Х1+5Х2=20, как Х2=4-4/5Х1 (число 20 произвольное). Обозначим эту линию РР. В каждой точке этой линии прибыль одинакова. Перемещая эту линию параллельно ее исходному положению, найдем точку, которая удалена от начала координат в наибольшей мере, однако, не выходит за пределы области допустимых решений. Это точка М0, которая лежит на вершине многоугольника. Координаты этой точки (![]() ) и будут искомым оптимальным планом.
) и будут искомым оптимальным планом.
Симплексный метод решения оптимизационных задач линейного программирования.
Симплексный метод – это вычислительная процедура, основанная на принципе последовательного улучшения решений при переходе от одной базисной точки (базисного решения) к другой. При этом значение целевой функции улучшается.
Базисным решением является одно из допустимых решений, находящихся в вершинах области допустимых значений. Проверяя на оптимальность вершину за вершиной симплекса, приходят к искомому оптимуму. На этом принципе основан симплекс-метод.
Симплекс – это выпуклый многоугольник в n-мерном пространстве с n+1 вершинами, не лежащими в одной гиперплоскости (гиперплоскость делит пространство на два полупространства).
Например, линия бюджетных ограничений делит блага на доступные и недоступные.
Доказано, что если оптимальное решение существует, то оно обязательно будет найдено через конечное число итераций (шагов), кроме случаев «зацикливания».
Алгоритм симплексного метода состоит из ряда этапов.
Первый этап. Строится исходная оптимизационная модель. Далее исходная матрица условий преобразуется в приведенную каноническую форму, которая среди всех других канонических форм выделяется тем, что:
а) правые части условий (свободные члены bi) являются величинами неотрицательными;
б) сами условия являются равенствами;
в) матрица условий содержит полную единичную подматрицу.
Если свободные члены отрицательные, то обе части неравенства умножаются на -1, а знак неравенства меняется на противоположный. Для преобразования неравенств в равенства вводятся дополнительные переменные, которые, обычно, обозначают объем недоиспользованных ресурсов. В этом их экономический смысл.
Наконец, если после добавления дополнительных переменных, матрица условий не содержит полную единичную подматрицу, то вводятся искусственные переменные, которые не имеют никакого экономического смысла. Они вводятся исключительно для того, чтобы получить единичную подматрицу и начать процесс решения задачи при помощи симплексного метода.
В оптимальном решении задачи все искусственные переменные (ИП) должны быть равными нулю. Для этого вводят искусственные переменные в целевую функцию задачи с большими отрицательными коэффициентами (-М) при решении задачи на max, и с большими положительными коэффициентами (+М), когда задача решается на min. В этом случае даже незначительное ненулевое значение искусственной переменной будет резко уменьшать (увеличивать) значение целевой функции. Обычно М в 1000 раз должно быть больше, чем значения коэффициентов при основных переменных.
Другие рефераты на тему «Экономико-математическое моделирование»:
Поиск рефератов
Последние рефераты раздела
- Выборочные исследования в эконометрике
- Временные характеристики и функция времени. Графическое представление частотных характеристик
- Автоматизированный априорный анализ статистической совокупности в среде MS Excel
- Биматричные игры. Поиск равновесных ситуаций
- Анализ рядов распределения
- Анализ состояния финансовых рынков на основе методов нелинейной динамики
- Безработица - основные определения и измерение. Потоки, запасы, утечки, инъекции в модели
