Построение неполной квадратичной регрессионной модели по результатам полного факторного эксперимента

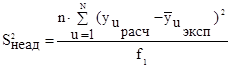Рефераты / Экономико-математическое моделирование / Построение неполной квадратичной регрессионной модели по результатам полного факторного эксперимента

; , (16)

где и - значения функции отклика в u-м эксперименте, соответственно рассчитанные по уравнению регрессии и определенные эксперим

ентально; f1 – число степеней свободы; - число оставленных коэффициентов уравнения регрессии, включая b0 (); N - число опытов плана (N = 8). Тогда f1 = 8 - 7 = 1.

Таким образом, если из регрессионной модели исключен, хотя бы один статистически незначимый коэффициент (а это неизбежно, если варьируемые факторы действительно являются независимыми переменными), массив разностей будет содержать информацию об ошибках в предсказании значений функции отклика.

Таблица 6

Сопоставление экспериментальных и расчетных данных

Номер эксперимента, u
1	97,3	66,36	30,94	957,3
2	127,6	96,7	30,9	954,8
3	153,7	183,16	-29,46	867,9
4	71,9	101,38	-29,48	869,1
5	113,7	84,22	29,48	869,1
6	91,8	62,32	29,48	869,1
7	127,1	157,98	-30,88	953,6
8	112,2	143,08	-30,88	953,6

В рассматриваемом случае построенная модель (15) включает шесть коэффициентов: . Тогда в соответствии с выражением (16) .

Гипотеза об адекватности модели (15) проверяется по критерию Фишера. Его расчетное значение находим по уравнению:

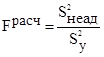. (17)

Из выражения (17) следует, что расчетное значение критерия Фишера представляет собой отношение дисперсии неадекватности к дисперсии опыта. По сути дела он позволяет ответить на вопрос: во сколько раз модель предсказывает значения функции отклика хуже по сравнению с опытом? Тогда табличное значение критерия Фишера должно регламентировать допустимое отклонение расчетных значений функции отклика относительно опытных данных.

Табличное значение критерия Фишера определяется в зависимости от уровня значимости a и числа степеней свободы f1 и f2, определенных ранее: F(a; f1; f2). При уровне значимости a = 0,05 табличное значение F - критерия (табл. В1, приложение В) равно .

7. Анализ модели

Все соображения о направлении и силе влияния изученных факторов на износостойкость чугунных тормозных колодок можно высказать только для выбранных интервалов их изменения.

Из анализа полученного уравнения регрессии (15), можно сделать вывод о том, что наиболее существенно увеличивает износостойкость фактор X3(С), а значит, для изготовления тормозных колодок следует использовать чугун с максимальным содержанием углерода: 3,8 мас. %.

Установлено, что наименьшие удельные потери массы (0,071 г/cм2) получены на образце № 7 (Al - 2,5 %, Mn - 12 %, С - 3,8 %) (табл. 6).

ПРИЛОЖЕНИЕ А

Таблица А1

Критические значения G-критерия (критерия Кохрена) при уровне значимости a = 0,05

Число опытов, N	Число степеней свободы,
Число опытов, N	1	2	3	4	5	6	7	8	9	10	16	36	144
2	0,999	0,975	0,939	0,906	0,858	0,853	0,833	0,816	0,801	0,788	0,734	0,66	0,581
3	0,967	0,871	0,798	0,746	0,707	0,677	0,653	0,633	0,617	0,603	0,547	0,475	0,403
4	0,907	0,768	0,684	0,629	0,59	0,56	0,537	0,518	0,502	0,488	0,437	0,372	0,309
5	0,841	0,684	0,598	0,544	0,506	0,478	0,456	0,439	0,424	0,412	0,365	0,307	0,251
6	0,781	0,616	0,532	0,48	0,445	0,418	0,398	0,382	0,368	0,357	0,314	0,261	0,212
7	0,727	0,561	0,48	0,431	0,391	0,373	0,356	0,338	0,325	0,315	0,276	0,228	0,183
8	0,68	0,516	0,438	0,391	0,36	0,336	0,319	0,304	0,293	0,283	0,246	0,202	0,162
9	0,64	0,478	0,403	0,358	0,329	0,307	0,29	0,277	0,266	0,257	0,223	0,182	0,145
10	0,602	0,445	0,373	0,331	0,303	0,282	0,267	0,254	0,244	0,235	0,203	0,166	0,131
12	0,541	0,392	0,326	0,288	0,262	0,244	0,23	0,219	0,21	0,202	0,174	0,14	0,11
15	0,471	0,335	0,276	0,242	0,22	0,203	0,191	0,182	0,174	0,167	0,143	0,114	0,089
20	0,389	0,271	0,221	0,192	0,174	0,16	0,15	0,142	0,136	0,13	0,111	0,088	0,068
24	0,343	0,235	0,191	0,166	0,149	0,137	0,129	0,121	0,116	0,111	0,094	0,074	0,057
30	0,293	0,198	0,159	0,138	0,124	0,114	0,106	0,1	0,096	0,092	0,077	0,06	0,046
40	0,237	0,158	0,126	0,108	0,097	0,089	0,083	0,078	0,075	0,071	0,06	0,046	0,035
60	0,174	0,113	0,09	0,077	0,068	0,062	0,058	0,055	0,052	0,05	0,041	0,032	0,023
120	0,1	0,063	0,05	0,042	0,037	0,034	0,031	0,029	0,028	0,027	0,022	0,017	0,012

Скачать реферат

Страница: 1 2 3 4 5 6 7 8 9 10 11

Построение неполной квадратичной регрессионной модели по результатам полного факторного эксперимента

Другие рефераты на тему «Экономико-математическое моделирование»:

Поиск рефератов

Последние рефераты раздела