Разработка системы учета и прогнозирования ежедневных поступлений страховых взносов на обязательное пенсионное страхование

Между величинами x и y существует функциональная зависимость, но ее аналитический вид обычно неизвестен, поэтому возникает практически важная задача - найти эмпирическую формулу

Формула 1

(где - параметры), значения которой при rc="images/referats/9780/image011.png">возможно мало отличались бы от опытных значений .

Обычно указывают класс функций (например, множество линейных, степенных, показательных и т.п.) из которого выбирается функция , и далее определяются наилучшие значения параметров.

Если в эмпирическую формулу 1 подставить исходные , то получим теоретические значения , где .

Разности называются отклонениями и представляют собой расстояния по вертикали от точек до графика эмпирической функции.

Согласно методу наименьших квадратов наилучшими коэффициентами считаются те, для которых сумма квадратов отклонений найденной эмпирической функции от заданных значений функции

Формула 2

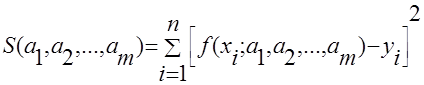
будет минимальной.

Поясним геометрический смысл метода наименьших квадратов.

Каждая пара чисел из исходной таблицы определяет точку на плоскости . Используя Формулу 1 при различных значениях коэффициентов можно построить ряд кривых, которые являются графиками функции (1). Задача состоит в определении коэффициентов таким образом, чтобы сумма квадратов расстояний по вертикали от точек до графика Функции 1 была наименьшей.

Построение эмпирической формулы состоит из двух этапов: выяснение общего вида этой формулы и определение ее наилучших параметров.

Если неизвестен характер зависимости между данными величинами x и y , то вид эмпирической зависимости является произвольным. Предпочтение отдается простым формулам, обладающим хорошей точностью. Удачный выбор эмпирической формулы в значительной мере зависит от знаний исследователя в предметной области, используя которые он может указать класс функций из теоретических соображений. Большое значение имеет изображение полученных данных в декартовых или в специальных системах координат (полулогарифмической, логарифмической и т.д.). По положению точек можно примерно угадать общий вид зависимости путем установления сходства между построенным графиком и образцами известных кривых.

Определение наилучших коэффициентов входящих в эмпирическую формулу производят хорошо известными аналитическими методами.

Для того, чтобы найти набор коэффициентов , которые доставляют минимум функции S , определяемой формулой (2), используем необходимое условие экстремума функции нескольких переменных - равенство нулю частных производных. В результате получим нормальную систему для определения коэффициентов :

Система 1

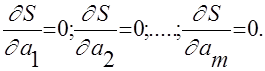
Таким образом, нахождение коэффициентов сводится к решению Системы 1.

Эта система упрощается, если эмпирическая Формула 1 линейна относительно параметров , тогда Система 1 будет линейной.

Конкретный вид Системы 1 зависит от того, из какого класса эмпирических формул мы ищем Зависимость 1. В случае линейной зависимости Система 1 примет вид:

Система 2

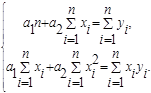
Эта линейная система может быть решена любым известным методом (методом Гаусса, простых итераций, формулами Крамера).

В случае квадратичной зависимости Система 1 примет вид:

Система 3

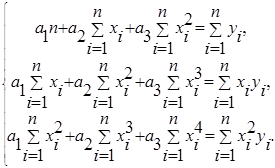
В ряде случаев в качестве эмпирической формулы берут функцию, в которую неопределенные коэффициенты входят нелинейно. При этом иногда задачу удается линеаризовать, т.е. свести к линейной. К числу таких зависимостей относится экспоненциальная зависимость

Формула 3

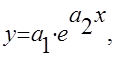
где и неопределенные коэффициенты.

Линеаризация достигается путем логарифмирования равенства (6), после чего получаем соотношение

Формула 4

Обозначим и соответственно через и , тогда зависимость (6) может быть записана в виде , что позволяет применить формулы (4) с заменой на и на .

1.3.1 Элементы теории корреляции

График восстановленной функциональной зависимости по результатам измерений называется кривой регрессии. Для проверки согласия построенной кривой регрессии с результатами эксперимента обычно вводят следующие числовые характеристики: коэффициент корреляции (линейная зависимость), корреляционное отношение и коэффициент детерминированности. При этом результаты обычно группируют и представляют в форме корреляционной таблицы. В каждой клетке этой таблицы приводятся численности тех пар , компоненты которых попадают в соответствующие интервалы группировки по каждой переменной. Предполагая длины интервалов группировки (по каждой переменной) равными между собой, выбирают центры (соответственно ) этих интервалов и числа в качестве основы для расчетов.

 Скачать реферат