Электромагнитные волны между параллельными идеально проводящими плоскостями

Очевидно, у нас нет оснований утверждать, что скорость распространения сигнала будет совпадать с фазовой скоростью. В самом деле, последняя, как было установлено, характеризует лишь фазовые соотношения между гармоническими колебаниями в различных точках пространства, когда эти колебания уже возникли и установились всюду.

Предположим, что в точке имеется сигнал, меняющийся во времени по закону . Выясним, какой вид будет иметь этот сигнал в других точках оси z при t > 0; иными словами, определим функцию , если известна функция , а также известны характеристики среды, в которой происходит распространение. Используя интеграл Фурье, представим в виде:

(1.33)

где — спектральная плотность функции . Согласно выражению (1.33) функция представляет собой сумму множества гармонических колебаний с частотами и амплитудами . Совокупность этих колебаний, как известно, образует спектр функции .

Но каждой составляющей при распространении колебаний вдоль оси z соответствует волна

где — волновое число. Поэтому функцию в любой точке оси z можно представить в виде

(1.34)

Из формулы (1.34) следует, что распространение сигнала в данном направлении обусловлено движением всех его гармонических составляющих.

В общем случае фазовая скорость волны зависит от частоты колебаний (подробнее об этом см. ниже). При наличии такой зависимости различные гармонические составляющие сигнала будут двигаться вдоль оси z с различными фазовыми скоростями. А это, очевидно, может привести к тому, что форма сигнала по мере его распространения будет изменяться.

Так как волновое число есть функция частоты, т. е. , в (1.34) вместо интегрирования по можно перейти к интегрированию по :

. (1.35)

Пусть действительный спектр сигнала ограничен частотами и , и, кроме того, (— средняя частота спектра). Тогда интегрирование в (1.34) будет происходить по промежутку , а в (1.35) — по промежутку . Здесь — среднее значение волнового множителя, соответствующее средней частоте и фазовой скорости на этой частоте, а . На основании этого вместо (1.35) будем иметь

(1.36)

Сигнал, определяемый интегралом (1.36), называется волновым пакетом или группой волн.

Рассматривая как функцию переменной , разложим в ряд по степеням :

(1.37)

и подставим из (1.37) в (1.36).

При малом промежутке интегрирования в разложении (1.37) можно ограничиться двумя первыми членами. В этом случае интеграл (1.36) принимает вид:

Здесь означает производную при .

Введя далее новую переменную интегрирования , получим

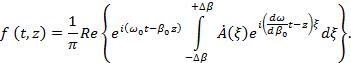
Будем полагать, что — непрерывная медленно меняющаяся функция. Тогда ее на малом интервале можно считать постоянной, равной . В этом случае

— аргумент комплексной величины .

Выражение (1.38), таким образом, определяет рассматриваемый сигнал в любой точке . Функция

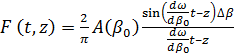(1.39)

вследствие того, что мало, является медленно меняющейся функцией переменных . Поэтому ее можно считать амплитудой волны . При функция является огибающей сигнала с узким (а точнее, с бесконечно узким) частотным спектром.

Из формулы (1.39) видно, что с течением времени огибающая перемещается вдоль оси . О ее движении удобно судить по перемещению максимума, находящегося в точке .

Нетрудно сообразить, что с течением времени этот максимум движется вдоль оси со скоростью

 Скачать реферат