Строительная механика

Содержание

1 Цель работы и решаемые задачи

2 Объект исследования

3 Динамическая система и метод расчета

3.1 Допущения по расчетной модели

3.2 Источник возмущений

3.3 Метод расчета и уравнения колебаний системы

3.4 Структура физико-математической модели динамической системы и ее топологическая модель

4 Инерционно-топологическая модель вагона

4.1 Характеристика инерционно-топологической подсистемы

4.2 Характеристики инерции

4.3 Математическая инерционная модель

5 Виброзащитная модель динамической системы

5.1 Характеристики рессорного подвешивания двухосной тележки грузового вагона

5.2 Нагруженность системы силами упругости и реакциями сил упругости

5.3 Математическая модель виброзащитной системы вагона

6 Внешняя нагруженность динамической системы

6.1 Физическая модель нагруженности вагона

6.2 Математическая модель внешних возмущающих нагрузок

6.3 Математическая модель динамики вагона на рессорах

7 Свободные колебания вагона на рессорах

7.1 Уравнения свободных колебаний вагона

7.2 Определение частот свободных колебаний

7.3 Формы колебаний вагона

8 Вынужденные колебания вагона на рессорах

8.1 Резонансные колебания кузова вагона

8.2 Определение параметров гасителей колебаний

Литература

1 Цель работы и решаемые задачи

Целью работы является:

- изучение метода расчета динамической системы;

- исследование колебаний вагона на рессорах.

Решаемые задачи:

- определение характеристик расчетных моделей подсистем;

- изучение свободных и вынужденных колебаний;

- определение параметров гасителей рессорного подвешивания вагона.

2 Объект исследования

Объектом исследования является модель крытого вагона 11-066 с одинарным рессорным подвешиванием.

Таблица 2.1

Характеристика задания

Таблица 2.2

Параметры модели кузова и груза

3 Динамическая система и метод расчета

3.1 Допущения по расчетной модели

При выборе динамической расчетной модели принимаем следующие допущения:

· динамическую систему представляем в виде системы твердых тел;

· полагаем, что в рессорном подвешивании отсутствуют диссипативные силы сухого и вязкого трения, система вследствие этого будет являться консервативной;

· грузы рассматриваем как твердые тела с жестким присоединением к кузову вагона;

· рессорные комплекты тележек имеют линейную силовую характеристику;

· путь считаем абсолютно жестким.

3.2 Источник возмущений

В качестве источника возмущения принимаем гармоническую неровность первого вида:

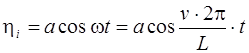,(3.1)

где - частота изменения гармонической неровности:

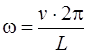,(3.2)

- скорость движения вагона.

3.3 Метод расчета и уравнения колебаний системы

Физическая модель метода расчета

Для расчета системы используем метод реактивных усилий. Колебания кузова в пространстве определяем по движению центра масс кузова : тремя линейными и тремя угловыми его перемещениями по направлению координатных осей кузова (рисунок 4.1).

Движение всех других частей кузова находим по колебаниям центра масс кузова и координатам этих частей, .

Узел , движение которого будем изучать, условимся называть центрально-координатным узлом.

Центрально-координатный узел полагаем имеет внутренние линейные и угловые связи по направлению координатных осей . Считаем, что все усилия, действующие на рассматриваемое тело, через внутренние элементы-вставки передаются в связи центрально-координатного узла и здесь взаимно уравновешиваются на основании принципа Лангранжа-Деламбера.

 Скачать реферат