Строительная механика

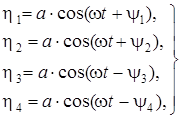,(6.1)

где – углы сдвига фаз в перемещениях колесных пар:

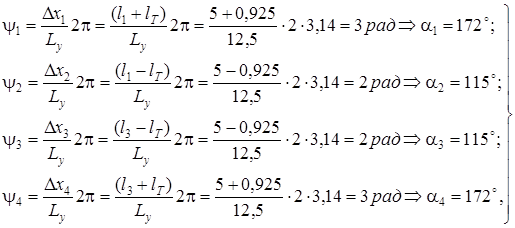,(6.2)

– амплитуда и длина волны вертикальной неровности пути;

– частота вынужденных кинематических возмущений,

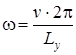(6.3)

При средней скорости движения вагона получим:

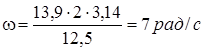
Перемещения буксовых узлов равны перемещениям точек контакта колес с рельсами (рисунок 6.1):

(6.4)

Из схем перемещений боковых рам находим перемещения нижних опорных поверхностей рессорных комплектов:

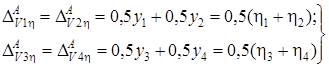(6.5)

Деформации и силы упругости в виброзащитных связях при значениях перемещений (6.5) составляют:

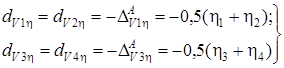(6.6)

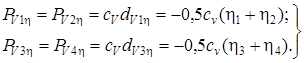(6.7)

Рисунок 6.2 – Расчетная схема для определения возмущающей нагрузки

6.2 Математическая модель внешних возмущающих нагрузок

Изначально силы упругости (6.7) в рессорном подвешивании на схемах (рисунок 6.2) положительны.

Силы упругости (6.7) вызывают в связях центрально-координатного узла кузова реакции возмущающих нагрузок (рисунок 6.2). Из равновесия кузова вектор кинематических возмущающих нагрузок равен:

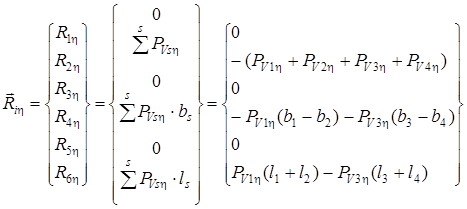,(6.8)

где .

При значениях сил (6.7) и (6.4) реакции (6.8) принимают значения:

(6.9)

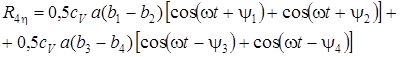(6.10)

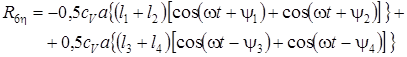(6.11)

В несимметричном вагоне возмущающие усилия вызывают колебания . Поскольку колебания через реакции связаны с , а последние через реакции с (5.12 ), то возникают все колебания кузова . Кузов испытывает сложные вынужденные колебания.

В симметричном вагоне при линейные реакции (6.9) не меняются, а угловые – (6.10), (6.11) становятся равными:

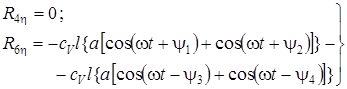(6.12)

Возмущающие реакции вызовут в системе колебания и . Колебание возникает вследствие взаимосвязи через реакции . Если реакции малы , то будем иметь только два вида колебаний - и .

В реакциях возмущения от колесных пар сдвинуты по фазе (), что создает некоторые затруднения в решении задачи. Для упрощения решения сложим составляющие гармонических возмущений в этих реакциях. Сложение выполним графическим способом, используя интерпретацию вращающихся векторов и их проекций на горизонтальную ось .

Рисунок 6.3 – Векторная диаграмма

Выполнив сложение векторов по тележкам, находим эквивалентную амплитуду вектора возмущений для вагона – , которая соответствует колебанию .

Из векторной диаграммы определяем: .

Проекция вектора на горизонтальную ось дает функцию суммарного возмущения на вагон:

(6.13)

Эта функция заменяет выражение, стоящее в фигурных скобках (6.9). Значение суммарной возмущающей реакции на вагон теперь равно:

(6.14)

 Скачать реферат