Метрические характеристики графа

Очевидно, что соответствие G→A(G) определяет биекцию множества помеченных графов порядка n на множество бинарных симметричных n×n-матриц с нулевой диагональю.

Аналогично определяются матрицы смежности A мульти - и псевдографов: ik равно числу ребер, соединяющих вершины i и k (при этом петля означает два ребра).

Также определяется матрица смежности A(G) ориентированного графа.

Очевидно, что если A(G) – матрица смежности орграфа G порядка n, то

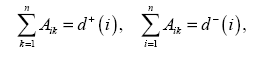
т.е. число единиц в i-й строке матрицы A(G) равно полустепени исхода i-й вершины, а число единиц в k-м столбце равно полустепени захода k-й вершины.

Теорема. Графы изоморфны тогда и только тогда, когда их матрицы смежности получаются друг из друга одинаковыми перестановками строк и столбцов.

Теорема верна также для мультиграфов, псевдографов и орграфов.

Пусть G –(n, m) - граф, VG={1, 2, ., n} EG={e1, e2, ., em}. Определим бинарную n×m-матрицу I=I(G) условиями

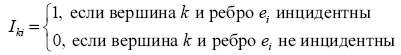
Матрица I называется матрицей инцидентности графа G. В каждом ее столбце ровно две единицы, равных столбцов нет. Как и выше, соответствие G→I(G) является биекцией множества помеченных (n, m) - графов с занумерованными ребрами на множество n×m-матриц, удовлетворяющих описанным условиям.

Матрица инцидентности I для орграфа:

Теорема. Графы изоморфны тогда и только тогда, когда их матрицы инцидентности получаются друг из друга произвольными перестановками строк и столбцов.

Теорема верна также для мультиграфов, псевдографов и орграфов.

Свойства матриц смежности и инцидентности:

1) Сумма элементов матрицы A(G), где G=(V, E) – мультиграф, V={v1, v2, ., vn}, по i-йстроке (или по i-му столбцу) равна δ(vi).2) Сумма элементов матрицы A(G), где G=(V, E) – ориентированный псевдограф,

V={v1, v2, ., vn}, по i-йстроке и по i-му столбцу соответственно равны δ(vi), δ(vi).

3) Пусть G– ориентированный мультиграф с непустым множеством дуг. Тогда: а) сумма строк матрицы I(G) является нулевой строкой; б) любая строка матрицы I(G) является линейной комбинацией остальных строк; в) ранг матрицы I(G) не превосходит n–1; г) для любого контура матрицы Gсумма столбцов матрицы I(G), соответст-вующих дугам, входящим в этот контур, равна нулевому столбцу.

4) Пусть G– мультиграф с непустым множеством ребер. Тогда при покоординат-ном сложении по модулю 2: а) сумма строк матрицы I(G) является нулевой строкой; б) любая строка матрицы I(G) является суммой остальных строк; в) для любого цикла в Gсумма столбцов матрицы I(G), соответствующих реб-рам, входящим в этот цикл, равна нулевому столбцу.

ОПЕРАЦИИ НАД ГРАФАМИ

Граф H называется подграфом графа G, если VHVG, EHEG. Если H – под-граф графа G, то говорят, что H содержится в G. Подграф называется собственным, если он отличен от самого графа.

Подграф H называется остовным подграфом графа G, если VH =VG.

Если множество вершин подграфа H есть U, а множество его ребер совпадает с множеством всех ребер графа G, оба конца которых принадлежат U, то H называется подграфом, порожденным множеством вершин U, и обозначается G(U).

Если множество ребер подграфа H есть E'EG, а множество его вершин совпадает с множеством всех концов ребер из E' вершин графа G, то подграф H называется подграфом, порожденным множеством ребер E' и обозначается G(E').

Пусть v – вершина графа G. Тогда операцию построения графа H=G–v называют удалением вершины v. Построенный в результате этой операции граф H содержит все ребра множества ЕG кроме инцидентных вершине v, а VH =VG\{v}.

Пусть e – ребро графа G. Тогда операцию построения графа H=G–e называют удалением ребра e. Построенный в результате этой операции граф H содержит все вершины графа G, а EH =EG\{e}.

Удаление вершины или ребра, а также переход к подграфу – это операции, с помощью которых можно из имеющегося графа получать другие графы с мень-шим числом элементов.

Рассмотрим теперь операции, позволяющие получать из имеющихся графов графы с большим числом элементов.

Если вершины u и v графа G=(VG, EG) не смежны, то говорят, что граф H=(VH, EH) получен из графа G добавлением ребра e={u, v}, если VH =VG и EH = EG{e}, то пишут H=G+e.

Граф H называется объединением (или наложением) графов F и G, если H =VF∩VG и EH =EF∩EG. В этой ситуации пишут H=F∩G. Объединение F∩G называется дизъюнктивным, если VF ∩ VG =∅. Аналогично определяются объединение и дизъюнктивное объединение любого множества графов, причем в последнем случае никакие два из объединяемых графов не должны иметь общих вершин.

Пусть G1=(V1, E1) и G2=(V2, E2). Тогда произведением графов (обозначается G1×G2) называется такой граф G, для которого VG =V1×V2– декартово произведе-ние множеств вершин исходных графов, а EG определяется следующим образом: вершины (u1, u2) и (v1, v2) смежны в графе G тогда и только тогда, когда u1=v1, а u2 и v2 смежны в G2, или u2=v2, а u1 и v1 смежны в G1

МАРШРУТЫ, ЦЕПИ, ЦИКЛЫ

Чередующаяся последовательность v1, e1, v2, e2, ., en, vn+1 вершин и ребер графа такая, что ei =vivi+1 (i=1, n), называется маршрутом, соединяющим вершины 1 и vn+1 (или (v1vn+1) - маршрутом). Очевидно, что для задания маршрута в графе достаточно задать последовательность v1, v2, ., vn+1. его вершин, либо последовательность e1, e2, ., en его ребер.

Вершина v называется достижимой из вершины u, если существует (u, v) - маршрут. Любая вершина считается достижимой из себя самой.

Маршрут называется цепью, если все его ребра различны, и простой цепью, если все его вершины, кроме, возможно, крайних, различны. Маршрут (1) называется циклическим, если v1=vn+1. Циклическая цепь называется циклом, а циклическая простая цепь – простым циклом. Число ребер в маршруте называется его длиной. Цикл длины 3 часто называют треугольником. Длина всякого цикла не менее трех, если речь идет о простом графе, поскольку в таком графе нет петель и кратных ребер. Минимальная из длин циклов графа называется его обхватом.

Свойства маршрутов, цепей и циклов:

1) Всякий незамкнутый (u, v) - маршрут, содержит в себе простую (u, v) - цепь. В частности, любая (u, v) - цепь, содержит в себе простую (u, v) - цепь. Причем, если (u, v) - маршрут содержит в себе вершину w (w≠u и w≠v), то в общем случае, простая (u, v) - цепь может не содержать в себе вершину w.

2) Всякий непростой цикл можно разбить на два или более простых. Причем для замкнутого маршрута такое утверждение не верно.

3) Всякая непростая (u, v) - цепь, может быть разбита на простую (u, v) - цепь и один или более простых циклов. Причем для незамкнутого маршрута такое утверждение не верно.

 Скачать реферат