Применение неравенств при решении олимпиадных задач

Теорема 2. Если x1, x 2, …, x n – положительные числа, то имеют место неравенства

An ≥ Gn ≥ Hn.

Действительно, применяя к числам неравенство Коши, получаем

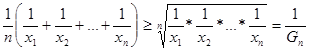, (3)

откуда Gn ≥ Hn.

Пусть x1, x 2, …, x n – произвольные числа. Средним

квадратическим этих чисел называется число –

.

Теорема 3. Если x1, x 2, …, x n – положительные числа, то имеют место неравенства

Kn ≥ An ≥ Gn ≥ Hn , или

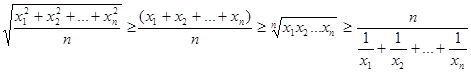. (4)

Причём знак равенства в (4) достигается тогда и только тогда, когда все числа равны.

Для двух чисел неравенство (4) можно записать как

,

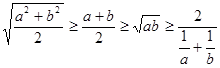которое очень легко доказать с помощью простых преобразований. А именно,

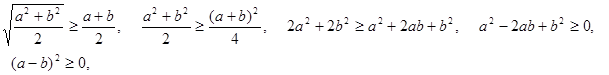
аналогично доказывается и для n чисел, откуда Kn ≥ An.

Неравенство Бернулли

Ещё один способ решения некоторых олимпиадных задач – это использование неравенства Бернулли, которое иногда может значительно облегчить задачу. «Классическое» неравенство Бернулли формируется следующим образом:

Теорема. Для x > -1 и произвольного натурального n имеет место

(1)

причем равенство в (1) достигается при x=0, n=0 или n=1.

Однако кроме (1) существует и более общее неравенство Бернулли, которое содержит в себе два неравенства:

если n<0 или n>1, то

, (2)

если 0<n<1, то

, (3)

где x > -1.

Следует отметить, что равенства (2) и (3) имеют место лишь при x=0.

Доказательство(I способ):

, где xi – числа одного и того же знака и .

Применяем метод математической индукции.

Проверяем неравенство для n=1: . Неравенство верно.

Пусть неравенство верно для n членов, т.е. верно неравенство

.

Умножим его на неотрицательное число 1+xn+1 (оно неотрицательно, т.к. ). Получим:

.

Т.к. xi одного знака, произведения в правой части положительны, и если их отбросить, неравенство только усилится. Получаем:

.

Как мы видим, неравенство верно и для n+1 членов, а значит верно для любых n.

Доказательство(II способ):

Также применяем метод математической индукции.

При n=1 имеем , . Утверждаем, что при n=k неравенство верно: . Тогда при n=k+1 имеем

.

Неравенство доказано.

Весовое (общее) неравенство Коши

Ранее мы рассмотрели так называемое классическое неравенство Коши. Однако очень большое значение имеет также одно важное обобщение неравенства Коши – это общее, или весовое, неравенство Коши.

Теорема. Для любых действительных положительных чисел m1, m2, …, mn и для любых неотрицательных x1, x2, …, xn имеет место неравенство

. (1)

Числа m1, m2, …, mn называются весовыми коэффициентами.

Неравенство (1) выполняется и для неотрицательных весовых коэффициентов m1, m2, …, mn, но в этом случае необходимо требовать, чтобы знаменатель левой части (1) не превращался в ноль и выражения имели смысл (т.е. не все m1, m2, …, mn равны нулю и числа xi и mi одновременно не равнялись нулю).

Понятно, что при m1= m2= …= mn, весовое неравенство Коши превращается в обыкновенное неравенство Коши.

Выражение, которое стоит в левой части (1), называется весовым средним арифметическим, а то, которое в правой – весовым средним геометрическим.

Неравенство (1), для натуральных m1, m2, …, mn, непосредственно следует из обыкновенного неравенства Коши:

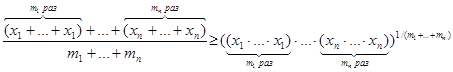. (2)

Неравенство (1) с неотрицательными рациональными весовыми коэффициентами легко привести к случаю, когда .

3.2 Решение задач с применением данных неравенств

Неравенство Йенсена

Задача:

Пусть a1,…, an > 0, . Доказать .

Решение:

Записываем неравенство Йенсена для f(x)=x2, mi=n. Получаем:

, , ,

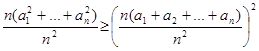что и требовалось доказать.

Неравенство Коши-Буняковского

Задача:

Пусть a+b+c=1. Доказать, что .

Решение:

Из неравенства Коши-Буняковского имеем

.

А отсюда имеем, что .

Неравенство Коши

Задача:

Пусть a, b, c – положительные числа, сумма которых равна единице. Доказать, что

(1+a)(1+b)(1+c) ≥ 8(1-a)(1-b)(1-c).

Решение:

Поскольку a+b+c=1, то 1+a= (1-b)+(1- c). Используя неравенство Коши между средним арифметическим и средним геометрическим , получаем

.

Аналогично

,

.

Перемножая все три неравенства, получаем искомое неравенство.

Неравенство Бернулли

Задача:

Решить уравнение

.

Решение:

К каждому слагаемому левой части уравнения применяем неравенство Бернулли, тогда

,

причем равенство возможно лишь при , т.е. x=±1. Следовательно, x=±1 – корни уравнения.

 Скачать реферат