Формирование понятия функции в курсе математики средней школы

f(x) = f(x - nT) доказано.

Число Т называется главным периодом, если оно положительно и является наименьшим среди всех положительных периодов, т.е. из положительных периодов функции y = f(x) (если он существует) называют её основным (главным периодом).

Рассмотрим примеры.

Пример №1. Функция y ={x} ({x} – дробная часть числа х) – периодическая. Заметим, что по определен

ию = х – [х], где [x] – целая часть числа х. Область определения данной функции - вся числовая прямая, поэтому для любого действительного числа х и любого Tx, Т0 числа (х + Т) и (х - Т) принадлежат области определения рассматриваемой функции и f(x +T ) = {x+T} = x + T – [x + T] = x + T –([x] + T) = x + T – [x] – T = x – [x] = {x}, где ТZ, T0.

Таким образом, функция у = {x} – периодическая с периодом Т, где ТZ, T0.

Наименьшее целое положительное число равно единице. Следовательно, основной период данной функции Т = 1.

Построим график функции у = {x}.

Для этого сначала построим график функции на промежутке х [0;1), длина которого равна основному периоду функции. Если х [0;1), то {x} = x, то есть на этом промежутке имеем у = х.

Весь график функции у = {x} получим параллельным переносом графика функции у = {x}, где х[0;1) вдоль оси абсцисс на = 1.

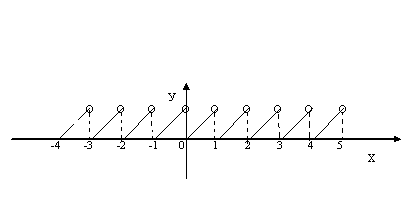
Пример № 2

Функция Дирихле – периодическая с периодом T = r, где r = Q.Действительно,

D(x) =

D(x + r) =

Так как r – рациональное число, то сумма х + r - рациональное число, как сумма двух рациональных чисел; с другой стороны, х + r - иррациональное число, как сума иррационального и рационального чисел.

Следовательно, D(x + r) = D(x).

Пример № 3

Функция y = sinне является периодической, так как, например для числа

х = 0 число (х – Т) при Т > 0 или число (х + Т) при Т < 0 не принадлежат области определения данной функции.

Пример № 4

Найти период функции

y = A sin (mx + ), где А, m, - постоянные величины, A0, m0,

x – аргумент.

Область определения функции – числовая прямая, поэтому числа (хТ)R, где Т0. Пусть основной период данной функции равен Т. Тогда для данной функции при любых действительных х рассмотрим равенство

A sin (m (x + T) + ) = A sin (mx + ).

Следовательно,

A (sin (m (x + T) + ) – sin (mx + ) = 0.

Применяя формулу разности синусов, будем иметь:

2А sincos = 0

2А sincos = 0

2А sincos = 0

2А sincos= 0

Это произведение должно равняться нулю независимо от значений х.

Так как х - переменная величина, то 2cos0, А0 по условию, тогда sin = 0, откуда следует

= , или , где nZ.

Из множества значений Т наименьшее положительное значение получим при наименьшем положительном значении n = 1, значит период данной функции

.

Заметим, что период функции у = А sin (mx + ) не зависит от A и .

Аналогично можно найти основные периоды и остальных тригонометрических функций.

Таким образом, функции

y = sin x и y = cos x имеют основной период Т = 2

у = tg x и у = ctg x имеют основной период Т = ,

а функции у = sin (mx + ) и у = cos(mx + ) имеют основной период Т = .

Функции у = tg (mx + ) и у = ctg (mx + ) имеют основной период Т = .

Отметим некоторые свойства периодических функций. Заметим, что сумма разность, произведение и частное двух периодических функций может быть функцией как периодической, так и не периодической.

Теорема 1. Если периодические функции y = f1 (x) и y = f2 (x), x Î X, имеют один и тот же период T, то их сумма, разность, произведение тоже будут периодическими функциями и число Т будет их периодом.

 Скачать реферат