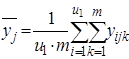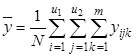Дисперсионный анализ при помощи системы MINITAB для WINDOWS
Если ![]() , то нулевая гипотеза отвергается и принимается альтернативная при соответствующем уровне значимости. Исходя из этого, можно сделать вывод о том, что исследуемый фактор оказывает существенное влияние на количественные данные.
, то нулевая гипотеза отвергается и принимается альтернативная при соответствующем уровне значимости. Исходя из этого, можно сделать вывод о том, что исследуемый фактор оказывает существенное влияние на количественные данные.
Результаты дисперсионного анализа сводятся в таблицу 2.
Таблица 2 Однофактор
ный дисперсионный анализ
|
Источник изменчивости | Сумма квадратов отклонений |
Число степеней свободы | Оценка дисперсии | F – отношение |
|
Между группами |
|
|
|
|
|
Внутри групп ( ошибка e) |
|
|
| |
|
Общая сумма |
|
|
|
![]() - число данных в столбце, u- число столбцов, m – число строк.
- число данных в столбце, u- число столбцов, m – число строк.
2.1.2. Двухфакторный дисперсионный анализ при перекрестной
классификации факторов
Часто необходимо качественно оценить значимость или незначимость влияния на целевую функцию u двух одновременно действующих факторов x1 и x2 . Такими факторами могут быть, например, форма собственности предприятия x1 и вид экономической деятельности x2.
Модель двухфакторного дисперсионного анализа имеет вид [1-4]:
![]()
где ![]() - общее среднее,
- общее среднее, ![]() -отклонение от общего среднего для фактора x1,
-отклонение от общего среднего для фактора x1, ![]() - отклонение от общего среднего для фактора x2,
- отклонение от общего среднего для фактора x2, ![]() - отклонение от общего среднего для взаимодействия двух факторов,
- отклонение от общего среднего для взаимодействия двух факторов, ![]() - случайная составляющая.
- случайная составляющая.
В этом случае общую сумму квадратов отклонений Q0 можно разбить на четыре суммы:
1) Qx1-по фактору x1,
2) Qx2-по фактору x2,
3) Qe-остаточную сумму квадратов, зависящую от ошибки e,
4) Q x1x2-зависящую от взаимодействия (произведения) x1x2 двух факторов.
В этом случае по выборочным значениям вычисляются:
1) среднее ![]() для каждого уровня фактора x1:
для каждого уровня фактора x1:
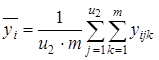 ;
;
2) среднее ![]() для каждого уровня фактора x2:
для каждого уровня фактора x2:
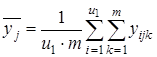 ;
;
3) общее среднее ![]() по всем N опытам, т.е. по всем m параллельным опытам на всех сочетаниях уровней факторов x1 и x2 (
по всем N опытам, т.е. по всем m параллельным опытам на всех сочетаниях уровней факторов x1 и x2 (![]() ):
):
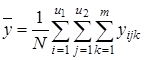 ;
;
4) среднее ![]() по m параллельным опытам для каждого сочетания уровней факторов x1 и x2:
по m параллельным опытам для каждого сочетания уровней факторов x1 и x2:
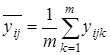 .
.
В табл.2 показаны данные полного факторного эксперимента с одинаковым числом наблюдений в ячейках.
Таблица 3. - Данные эксперимента и расчёты средних при двухфакторном дисперсионном анализе
|
j = |
1 |
2 |
… |
|
| |
|
|
k |
|
|
… |
| |
|
1 |
1 |
| ||||
|
2 |
| |||||
|
… |
… | |||||
|
m |
| |||||
|
. . . |
1 | |||||
|
2 | ||||||
|
… | ||||||
|
m | ||||||
|
|
1 | |||||
|
2 | ||||||
|
… | ||||||
|
m | ||||||
|
|
| |||||
Другие рефераты на тему «Экономико-математическое моделирование»:
Поиск рефератов
Последние рефераты раздела
- Выборочные исследования в эконометрике
- Временные характеристики и функция времени. Графическое представление частотных характеристик
- Автоматизированный априорный анализ статистической совокупности в среде MS Excel
- Биматричные игры. Поиск равновесных ситуаций
- Анализ рядов распределения
- Анализ состояния финансовых рынков на основе методов нелинейной динамики
- Безработица - основные определения и измерение. Потоки, запасы, утечки, инъекции в модели

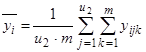
 i =
i =