Закономерность распределения простых чисел в ряду натуральных чисел

Простые числа? – Это просто!?

Узнав о важной роли простых чисел (ПЧ) в криптографии, генерации случайных чисел, навигации, имитационном моделировании и о том, что нужна закономерность распределения ПЧ в ряду натуральных чисел, не являясь математиком, всё же рискнул заняться решением этой задачи. Результат ниже.

Для начала выписал ряд ПЧ. Конечно же, это было сделано с целью заметить,

хоть какую бы, закономерность. С этой же целью были вычислены разности между соседними числами ряда ПЧ. Было замечено, что иногда появлялась последовательность разностей 6-4-2-4-2-4-6-2. Там, где эта последовательность нарушалась, были введены составныё числа (СЧ). Результат представлен в таблице 1, СЧ в которой подчёркнуты. Числа 2, 3, 5, являясь ПЧ, из рассмотрения всё же были убраны. Это первое исключение из правил. Вторая вольность заключалась введением в рассмотрение числа 1, зная, что единица не является простым числом.

Целью же было найти закономерность среди ПЧ + СЧ, а потом уже найти закономерность среди ПЧ. Стратегия поиска закономерности ПЧ заключалась в следующей логической формуле:

(закономерность ПЧ+СЧ) – (закономерность СЧ) = закономерность ПЧ.

Из ПЧ + СЧ, представленных в таблице 1, была составлена система из восьми арифметических прогрессий. Результат представлен в таблице 2.

Разности всех восьми прогрессий равны 30 и их первые члены равны соответственно 1, 7, 11, 13, 17, 19, 23, 29, а сами ряды обозначены через R1, R7,R11, R13, R17, R19, R23, R29. СЧ, как и в таблице 1, подчёркнуты и сверху расписаны в виде произведений двух чисел. Можно сформулировать правило, по которому в любой из восьми арифметических прогрессий распределены СЧ.

Если в арифметической прогрессии, какой – либо член an можно представить в виде двух сомножителей fxp, то последующие члены этой прогрессии an+mf являются произведением fx(p+md), а члены an+kp произведением px(f+kd), где m и k любые натуральные

числа, а d – разность этой прогрессии.

Данное правило не нуждается в доказательстве, т. к. фактически следует из определения арифметической прогрессии. Но для обеспечения закономерности ПЧ имеет большое значение. Во - первых, оно запрещает поиск рядов ПЧ, подчиняющихся одной арифметической прогрессии, т. к. любое простое число an можно представить в виде anх1, и тогда в любом ряде через число членов an, появляется составное число anх(1+d).

Во – вторых, в любой арифметической прогрессии появление дополнительных составных чисел возможно только в сочетании с разностью именно этой прогрессии.

Это правило можно сформулировать для любого числа сомножителей, но в данном случае интерес представляет число сомножителей равное двум.

В качестве примера рассмотрим в ряде R1 четвёртый член равный 91=7х13. Ближайшим членом в ряде R1 кратным семи является число 301, отстоящее от числа 91 на семь номеров, соответственно, число 301 принадлежит ряду СЧ. Число 301 является произведением 7х43 (301=7х43), и с номера этого числа равного 11, каждое сорок третье число, тоже делится на 43 и, соответственно, принадлежит к ряду СЧ. Дальше это можно не описывать, т. к. это хорошо видно в таблице 2.

Расписав таблицу 2 в виде математических символов, удалось получить систему из восьми формул, расписанных в виде разности сумм, см. таблицу 3. Во всех восьми формулах системы, члены с рядами двойных сумм служат фильтрами, удаляющими СЧ из ряда ПЧ+СЧ, и задают работу фильтров в виде матриц.

В таблице 4 изображено распределение номеров СЧ в ряде R1, определяемых вторым членом формулы. Это матрица, в которой и по столбцам и по строкам арифметические прогрессии.

В формулах индексы и обозначают столбцы и строки подобных матриц, сами же и дополнительными индексами не отягощаю. Без и описать работу матриц не смог, а формальная фраза, что в выражении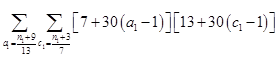под суммой произведений подразумеваются всевозможные их комбинации в зависимости от значений a1 и с1, будет неверна. Ибо все члены с номерами при >1 и >1 из формулы выпадают.

Система формул арифметических прогрессий, позволяющая вычислять ПЧ, получилась достаточно громоздкой, но закономерность обозначена.

Данная статья была подготовлена для публикации в научном журнале с математическим уклоном. Пока шёл поиск данного журнала, путём несложных умозаключений, была составлена система рядов арифметических прогрессий с разностью 10. Результат в таблице 5 и 6. Всё было расписано по образцу и подобию предыдущего материала. В таблице 7 изображена матрица для номеров второго члена формулы 1 таблицы 6.

Не начав переписывать статью заново, в связи с открытием новой системы уравнений, опять же путём размышлений, были расписаны арифметические прогрессии с разностью 2 и 1, т.е. при разности единица ПЧ были напрямую увязаны с натуральным рядом. Результат в таблице 8 и 9.

Всё расписано, как и в случаях с системами уравнений арифметических прогрессий разностей 30 и 10. И после этого наступил момент истины.

Оказалось, что подобных уравнений можно составить бесконечное множество. Навскидку – это арифметические прогрессии с разностью 1, 2, 4, 6, 10, 12, 18, 20, 30, 36, 60, и т.д. Даже в перечисленном до разности 60 указаны не все.

Обобщающий вывод:

ПЧ можно представить комбинацией арифметических прогрессий. Таких комбинаций бесконечное множество. Но каждая из комбинаций систем арифметических прогрессий позволяет только единственное представление ПЧ при заданной разности прогрессий задающий ряды ПЧ+СЧ.

 Скачать реферат