Законы больших чисел

U1, U2, ., Un. Кроме того, при , и, следовательно, для произвольного > 0 и всех достаточно больших n

. (2.6)

Далее, из (2.5) и (2,4) следует, что

(2.7)

Uk взаимно независимы, и с их суммой U1+U2+…+Un можно поступить точно так же, как и с Xk в случае конечной дисперсии, применив неравенство Чебышева, мы получим аналогично (2.1)

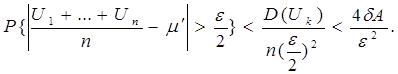(2.8)

Вследствие (2.6) отсюда вытекает, что

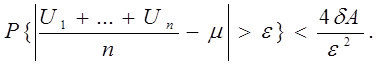(2.9)

Далее заметим, что с большой вероятностью Vk = 0. Действительно,

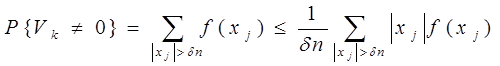(2.10)

Поскольку ряд (2.4) сходится, последняя сумма стремится к нулю при возрастании n. Таким образом, при достаточно большом п

P{Vk0} (2.11)

и следовательно

P{V1+…+Vn0}. (2.12)

Но , и из (2.9) и (2.12) получаем

(2.13)

Так как и произвольны, правая часть может быть сделана сколь угодно малой, что и завершает доказательство.

Теория «безобидных» игр

При дальнейшем анализе сущности закона больших чисел будем пользоваться традиционной терминологией игроков, хотя наши рассмотрения допускают в равной степени иболее серьезные приложения, а два наших основных предположения более реальны в статистике и физике, чем в азартных играх. Во-первых, предположим, что игрок обладает неограниченным капиталом, так что никакой проигрыш не может вызвать окончания игры. (Отбрасывание этого предположения приводит к задаче о разорении игрока, которая всегда интригует изучающих теорию вероятностей.) Во-вторых, предположим, что игрок не имеет нрава прервать игру, когда ему заблагорассудится: число п испытаний должно быть фиксировано заранее и не должно зависеть от хода игры. Иначе игрок, осчастливленный неограниченным капиталом, дождался бы серии удач и в подходящий момент прекратил бы игру. Такого игрока интересует не вероятное колебание в заданный момент, а максимальные колебания в длинной серии партий, которые описываются скорее законом повторного логарифма, чем законом больших чисел .

Введем случайную величину k как (положительный или отрицательный) выигрыш при k-м повторении игры. Тогда сумма Sn =1+…+k является суммарным выигрышем при п повторениях игры. Если перед каждым повторением игрок уплачивает за право участия в игре (не обязательно положительный) взнос , то ппредставляет собой общий уплаченный им взнос, a Sn — побщий чистый выигрыш. Закон больших чисел применим, если p=M(k) существует. Грубо говоря, при больших п весьма правдоподобно, что разность Sп — покажется малой по сравнению с п. Следовательно, если меньше, чем р, то при больших п игрок будет, вероятно, иметь выигрыш порядка . По тем же соображениям взнос практически наверняка приводит к убытку. Короче, случай благоприятен для игрока, а случай неблагоприятен.

Заметим, что мы еще ничего не говорили о случае. В этом случае единственно возможным заключением является то, что при достаточно большом и общий выигрыш или проигрыш Sn — пбудет с очень большой вероятностью малым по сравнению с п. Но при этом неизвестно, окажется ли Sn — пположительным или отрицательным, т. е. будет ли игра выгодной или разорительной. Это не было учтено классической теорией, которая называла безобидной ценой, а игру с «безобидной». Нужно понимать, что «безобидная» игра может на самом деле быть и явно выгодной и разорительной.

Ясно, что в «нормальном случае» существует не только M(k), но и D(k). В этом случае закон больших чисел дополняется центральной предельной теоремой, а последняя говорит о том, что весьма правдоподобно, что при «безобидной» игре чистый выигрыш в результате продолжительной игры Sn — пбудет иметь величину порядка n1/2 и что при достаточно больших п этот выигрыш будет с примерно равными шансами положительным или отрицательным. Таким образом, если применима центральная предельная теорема, то термин «безобидная» игра оказывается оправданным, хотя даже и в этом случае мы имеем дело с предельной теоремой, что подчеркивается словами «в результате продолжительной игры». Тщательный анализ показывает, что сходимость в (1.3) ухудшается при возрастании дисперсии. Если велико, то нормальное приближение окажется эффективным только при чрезвычайно больших п.

Для определенности представим машину, при опускании в которую рубля игрок может с вероятностью 10 выиграть (10—1) рублей, а в остальных случаях теряет опущенный рубль. Здесь мы имеем испытания Бернулли и игра является «безобидной». Проделав миллион испытаний, игрок уплатит за это миллион рублей. За это время он может выиграть 0, 1,2, . раз. Согласно приближению Пуассона для биномиального распределения, с точностью до нескольких десятичных знаков вероятность выиграть ровно к раз равна e-1/k!. Таким образом, с вероятностью 0,368 . . . игрок потеряет миллион, и с той же вероятностью он только окупит свои расходы; он имеет вероятность 0,184 . приобрести ровно один миллион и т. д. Здесь 106 испытаний эквивалентны одному-единствеиному испытанию при игре с выигрышем, имеющим распределение Пуассона.

 Скачать реферат