Проблема обучения математике в профильных классах на примере темы "Логарифмические уравнения"

Ответ: ,

5) .

Решение:

. Проведём некоторые упрощения:

ht=41 src="images/referats/29668/image203.png">

Поэтому уравнение имеет вид:

Прологарифмируем обе части уравнения по основанию x:

Обозначим . Тогда

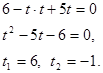
Следовательно: или

и

Ответ: , .

6) .

Решение:

ОДЗ:

В одной и той же системе координат строим графики функций и

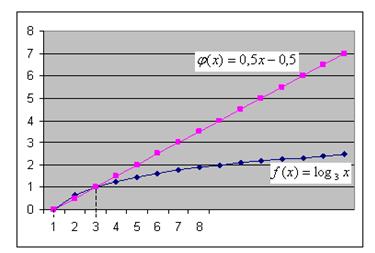
Абсциссы точек пересечения графиков функций и равны примерно 1 и 2. Нетрудно проверить, что это корни данного уравнения.

Проверка: - верное равенство,

- верное равенство.

Ответ: , .

Задание 5: Тестовое задание:

1) а;

2) в;

3) г;

4) а.

Решение тестового задания:

Решите уравнение:

1) .

Решение:

Данному уравнению удовлетворяют те значения x, для которых выполнено равенство . Мы получили квадратное уравнение , корни которого равны и . Следовательно, числа и - решения данного уравнения.

Ответ: , .

2) .

Решение:

Это уравнение определено для тех значений x, при которых выполнены неравенства и . Для этих x данное уравнение равносильно уравнению , из которого находим . Число не удовлетворяет, однако, неравенству . Следовательно, данное уравнение корней не имеет.

Ответ: корней нет.

3) . (1)

Решение:

Учитывая, что , преобразуем данное уравнение к виду (2)

Это уравнение, как легко установить, имеет решения , .

Обратим внимание на то, что в уравнении (2), выражение определено для всех , в то время как в исходном уравнении (1) соответствующее выражение определено лишь при . Проверка показывает, что из двух решений уравнения (2) лишь является решением уравнения (1).

Ответ: .

4) .

Решение:

Обозначим: , получаем уравнение

Ответ:

Задание 7: Решите уравнения:

.

Решение:

Потенцируя по основанию 2, получаем

Подставляя эти решения в уравнение, убеждаемся в том, что они являются решениями и этого уравнения.