Проблема обучения математике в профильных классах на примере темы "Логарифмические уравнения"

.

Но

Ответ:

Задание 8: Проверьте решение уравнений по листу самоконтроля, и в соответствии с набранными баллами поставьте себе оценку.

25-29 баллов -

оценка "5",

20-25 баллов - оценка "4",

13-19 баллов - оценка "3".

Задание 9: Выполните предложенную самостоятельную работу, выбирая тот вариант, который вы решите сами (самостоятельная работа находится в модульной карте и рассчитана на три уровня: на "3", "4", "5").

(5), (1)

Решение:

(1) запишется в виде

, то есть .

Решаем это уравнение методом введения новой переменной. Положим , получим: , корни которого , .

Теперь задача свелась к решению совокупности двух уравнений: ; .

Из первого уравнения получаем , откуда .

Из первого уравнения получаем , откуда .

Проверка показывает, что оба найденных значения и являются корнями уравнения (1).

Приложение 2

Решение задания из ЕГЭ и "нестандартного уравнения"

Пример: Найдём все значения , при которых уравнение

. (1)

имеет единственный корень.

Решение:

Преобразуем уравнение к виду .

Далее получаем , откуда

. (2)

Уравнение (1) имеет единственный корень в следующих случаях:

уравнение (2) имеет единственный корень и этот корень удовлетворяет уравнению (1);

уравнение (2) имеет два корня, но из этих корней один является посторонним для уравнения (1).

Рассмотрим первый случай. Уравнение (2) имеет один корень, если его дискриминант D равен нулю. Имеем

.

при или при . Случай, когда , отпадает, так как при правая часть уравнения (1) не определена. Если , то из уравнения (2) находим - единственный корень уравнения (2) и, как показывает проверка, удовлетворяющий и уравнению (1).

Рассмотрим второй случай, когда . В этом случае уравнение (2) имеет два корня:

.

Чтобы найденные корни были корнями уравнения (1), необходимо и достаточно, чтобы они удовлетворяли неравенству . Значит, из найденных корней уравнения (2) один будет корнем уравнения (1), а другой не будет корнем этого уравнения тогда и только тогда, когда

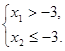или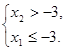

где , .

Решим первую систему. Имеем:

откуда имеем , то есть .

Решим вторую систему. Имеем:

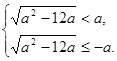
Эта система не имеет решений, так как либо , либо , то есть либо первое, либо второе неравенство последней системы не имеет решений. Итак, второй случай имеет место при .

Окончательно получаем, что уравнение (1) имеет единственный корень, если или если .

При наличии времени на уроках рекомендуется рассмотреть так называемые "нестандартные уравнения". Приведём пример такого уравнения:

Пример: Решить уравнение

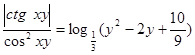. (1)

Решение:

Заметив, что , а , перепишем уравнение (1) в виде

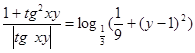. (2)

Нетрудно показать, что 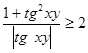. Для этого достаточно переписать это неравенство в виде 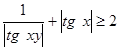и воспользоваться неравенством , если . В то же время . В самом деле, , а (тогда в силу убывания функции ) .