Разработка темы "Производная в школьном курсе математики"

Теперь используя формулу перехода к другому основанию, получим: . Теперь найдем производную этой функции:

.

Задача 4. Найти производную функции .

Решение. По правилу дифференцирования слож

ной функции получаем:

Задания для самостоятельной работы: найти производные функций: а)

; б) ; в) ; г) ; д) ;

Урок 4.

Тема: Касательная к графику функции.

Цели:

-образовательная: рассмотреть понятие касательной и ее уравнение;

-развивающая: углубить знания по теме;

-воспитательная: формирование умения анализировать.

Тип занятия: комбинированный.

Вид занятия: практикум.

Материал к занятию.

Пусть мы имеем кривую и на ней фиксированную точку . Возьмем на кривой точку и проведем секущую (рис. 1). Если точка неограниченно приближается по кривой к точке , то секущая занимает различные положения , и т.д.

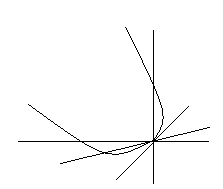
Рис. 1

Если при неограниченном приближении точки по кривой к точке с любой стороны секущая стремится занять положение определенной прямой , то прямая называется касательной к кривой в точке .

Кроме того, нетрудно установить, что значение производной , где - функция, задающая данную кривую, при данном значении аргумента равняется тангенсу угла, образованного с положительным направлением оси касательной к графику функции в соответствующей точке .

В этом заключается геометрический смысл производной.

Выведем теперь уравнение касательной к графику функции в точке .

Уравнение прямой с угловым коэффициентом имеет вид:

.

Для вычисления воспользуемся тем, что касательная проходит через точку :

, откуда ,

значит, уравнение касательной имеет вид:

или

.

Задача 1. Найти тангенсы углов наклона касательной к кривой в точках

Решение. Используя геометрический смысл производной, получим:

для точки : ;

для точки : .

Задача 2. Найти уравнение касательной к касательной к графику функции в точке с абсциссой 2.

Решение. Здесь . Подставляя эти числа в уравнение касательной, получим:

т.е.

.

Задача 3. вывести уравнение касательной к параболе в точке с абсциссой .

Решение. Имеем , а . Подставляя эти значения в уравнение касательной, получаем , т.е. . Например, при получаем касательную, имеющую уравнение .

Найдем координаты точки пересечения касательной к параболе в точке осью абсцисс. Если - координаты точки , то, поскольку принадлежит касательной, имеем . Если , то .