Разработка темы "Производная в школьном курсе математики"

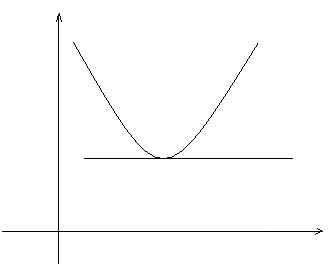
Рис. 5

Из теоремы 1 непосредственно вытекает следствие: если при всех рассматриваемых значениях арг

умента функция имеет производную, то она может иметь экстремум только при тех значениях, при которых производная обращается в нуль. Обратное заключение неверно: не при всяком значении, при котором производная обращается в нуль, обязательно существует максимум или минимум.

Кроме того, функция может достигать максимума или минимума в тех точках, где производная терпит разрыв. Заметим, что если производная не существует в какой-либо точке (но существует в близлежащих точках), то в этой точке производная терпит разрыв.

Таким образом, функция может иметь экстремум лишь в двух случаях: либо в тех точках, где производная существует и равна нулю; либо в тех точках, где производная не существует.

Значения аргумента, при которых производная обращается в нуль или не существует, называются критическими точками или критическими значениями.

Задача 1. Найти точки экстремума функции .

Решение. Производная этой функции равная , определена во всех точках и обращается в нуль при и . В точке производная меняет знак с минуса на плюс. В точке производная меняет знак с плюса на минус. Значит, при функция имеет минимум, а при - максимум.

Задача 2. Исследовать на максимум и минимум функцию

.

Решение. Находим первую производную:

Находим ее корни:

При переходе через значение производная меняет знак с плюса на минус. Следовательно, при функция имеет максимум.

При переходе через значение производная меняет знак с минуса на плюс. Следовательно, при функция имеет минимум.

Задача 3. Найти наименьшее значение функции .

Решение. Эту задачу можно решить, используя производную функции. Однако эту задачу можно решить и элементарным способом, тем более применяемый здесь прием приемлем для решения многих типов задач.

Функцию представим в виде:

.

Числа являются положительными, поэтому

.

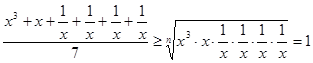Отсюда следует, что , когда все члены равны между собой

Тогда .

Задания для самостоятельной работы: найти минимумы и максимумы функций: а) ; б) ; в) ; г) ;

Урок 8.

Тема: Применение производной к исследованию функций.

Цели:

-образовательная: рассмотреть применение производной к исследованию функций;

-развивающая: углубить знания по теме;

-воспитательная: воспитание внимания и умения анализировать полученное решение, участвовать в диалоге с товарищами, учителем.

Тип занятия: изучение нового материала.

Вид занятия: практикум.

Материал к занятию.

Задача 1. Исследовать функцию

.

Решение.

Находим первую производную:

.

Находим критические значения аргумента:

a) находим точки, в которых функция обращается в нуль:

.

b) находим точки, в которых производная терпит разрыв (в данном случае обращается в бесконечность). Такой точкой будет, очевидно, точка:

.

(отметим, что при рассматриваемая функция определена и непрерывна). Других критических точек нет.

Исследуем характер полученных критических точек. Исследуем точку

.

Заметим, что

, .

Заключаем, что при функция имеет минимум. Значение функции в точке минимума равно

.

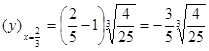Исследуем вторую критическую точку

.

Заметив, что

, ,

Заключаем, что при функция имеет максимум , причем

.

График исследуемой функции изображен на (рис. 6).