Разработка темы "Производная в школьном курсе математики"

а) найти значение функции на концах отрезка и в критических точках;

б) если на отрезке одна критическая точка, то ее подвергают исследованию на максимум и минимум и делают вывод.

. В этом случае следует поступать следующим образом:

а) вместо интервала берут отрезок и поступают, так как в п. 1а и если наибольшее значение достигается в концевой точке, то наибольшего значения нет;

б) если на наибольшее значение достигается внутри отрезка, то оно и будет наибольшим значением на интервале;

в) если на интервале одна критическая точка, то поступаем как в случае 1б.

Пусть , тогда:

а) если на этом промежутке более одной критической точки, то бесконечный интервал разбивается на два: конечный и бесконечный. На бесконечном промежутке помещают только одну критическую точку. Все остальные помещаются в конечный.

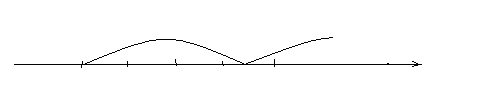
Рис. 10

б) если на бесконечном интервале одна критическая точка, то ее подвергают исследованию на минимум и максимум и делают вывод.

Задача 2. Какие размеры нужно придать цилиндру, чтобы при данном объеме его полная поверхность была наименьшей.

Решение. Обозначая через радиус основания цилиндра и через высоту цилиндра, будем иметь

.

Так как объем цилиндра задан, то при данном радиусе величина определяется формулой

откуда

.

Подставляя это выражение в формулу для , получим

Здесь - заданное число. Таким образом, мы представили как функцию одного независимого переменного .

Найдем наименьшее значение этой функции в промежутке :

.

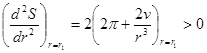Следовательно, в точке функция имеет минимум. Заметив, что и , т.е. что при стремлении к нулю или к бесконечности поверхность неограниченно возрастает, приходим к выводу, что в точке функция имеет наименьшее значение.

Но если , то

.

Таким образом, для того, чтобы при данном объеме полная поверхность цилиндра была наименьшей, высота цилиндра должна равняться диаметру.

Часто также встречаются текстовые задачи на экстремумы, особенно на вступительных и выпускных экзаменах и, в частности ЕГЭ. Алгоритм решения таких задач выглядит так:

укажите в задаче все постоянные величины, переменные величины и величину, которая исследуется;

из всех переменных величин одну выбрать за независимую и указать область ее изменения;

величину исследуемую задачей выразить через выбранную независимую переменную

найдите критические точки полученной функции на области изменения е аргумента

найдите наибольшее или наименьшее значение этой функции

выбрав наименьшее или наибольшее значение, ответьте на вопрос задачи.

Задача 3. Корабль отстает от берега (точка А) на расстоянии 3 км. С корабля отправлен гонец с донесением в штаб В, находящегося от точки А по берегу на расстоянии 10 км. К какому пункту берега должна пристать лодка, чтобы донесение в штаб было доставлено в кратчайшее время. Если .

Решение.

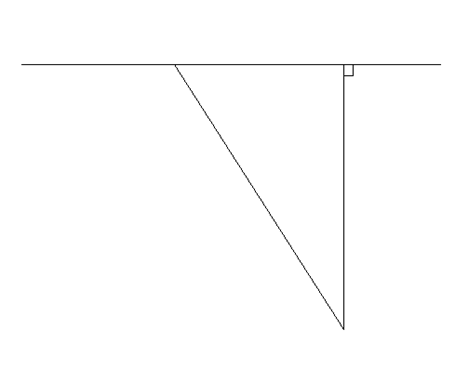
Рис. 11.

АВ, АК, ;

АМ, МВ, КМ – переменные величины;

;

;

Находя производную и приравнивая ее к нулю, находим критическую точку . Явно видно, что эта точка минимума.