Некоторые задачи оптимизации в экономике

u(x1,x2)→max

при ограничении p1x1+p2x2≤Q

и условие x1≥0, x2≥0.

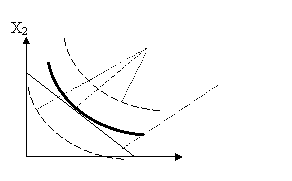
Допустимое множество (т.е. множество наборов продуктов, доступных для потребителя) представляет собой треугольник, ограниченный осями координат и бюджетной прямой. На этом множестве требуется найти точку, принадлежащую кривой безразличия с максимальным уровнем полезности. Поиск этой

точки можно интерпретировать графически как последовательный переход на линии всё более высокого уровня полезности до тех пор, пока эти линии ещё имеют общие точки с допустимым множеством.

2) Решение задачи потребительского выбора и его свойства.

Набор (х, х), который является решением задачи потребительского выбора, принято называть оптимальным для потребителя.

Рассмотрим некоторые свойства задачи потребительского выбора. Во – первых, решение задачи (х, х) сохраняется при любом монотонном (т.е. сохраняющем порядок значении) преобразовании функции полезности u(x1,x2). Поскольку значение u(х, х), было максимальным на всём допустимом множестве, оно остаётся таковым и после монотонного преобразования функции полезности (допустимое множество, определяемое бюджетным ограничением, остаётся неизменным). Таким монотонным преобразованием может быть умножение функции полезности на некоторое положительное число, возведение её в положительную степень, логарифмирование.

Во – вторых, решение задачи потребительского выбора не изменится, если все цены и доход увеличиваются (уменьшаются) в одно и то же число раз λ . (λ>0)

Это равнозначно умножению на положительное число λ обеих частей бюджетного ограничения p1x1+p2x2≤Q, что даёт неравенство, эквивалентное исходному. Поскольку ни цены, ни доход Q не входят в функцию полезности, задача остаётся той же, что и первоначально.

Если на каком – то потребительском наборе (x1,x2) бюджетное ограничение p1x1+p2x2≤Q будет выполнятся в виде строгого неравенства, то мы можем увеличить потребление какого – либо из продуктов и тем самым увеличить функцию полезности. Следовательно, набор (х, х), максимизирующий функцию полезности, должен обращать бюджетное ограничение в равенство, т.е. p1х+p2х=Q.

Графически это означает, что решение (х, х) задачи потребительского выбора должно лежать на бюджетной прямой, которая проходит через точки пересечения с осями координат, где весь доход тратиться на один продукт: (0, ) и (,0).

Итак, задачу потребительского выбора можно заменить задачей на условный экстремум (ибо решение (х, х) этих двух задач одно и то же)

u(x1,x2)→max

при условии p1x1+p2x2=Q.

Для решения этой задачи применим метод Лагранжа. Выписываем функцию Лагранжа L(x1,x2, λ)= u(x1,x2)+ λ (p1x1+p2x2-Q), находим её частные производные по переменным x1,x2 и λ и приравниваем к нулю:

L= u+λ p1=0,

L= u +λ p2 =0,

L=p1x1+p2x2-Q =0.

Исключив из полученной системы неизвестную λ, получим систему двух уравнений с двумя неизвестными x1, и x2

=,

p1x1+p2x2=Q .

Решение (х, х) этой системы есть критическая точка функции Лагранжа. Подставив решение (х, х) в левую часть равенства

=,

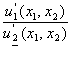получим, что в точке (х, х) отношение предельных полезностей u(х, х) и u(х, х) продуктов равно отношению рыночных цен p1 и p2 на эти продукты:

 Скачать реферат