Некоторые задачи оптимизации в экономике

Найти план выпуска изделий, обеспечивающий предприятию наивысшую прибыль в условиях нарушения баланса между объёмом и оптимальным размером предприятия.

Решение: Составим математическую модель задачи.

Пусть Z – прибыль, получаемая предприятием после реализации х1 выпущенных изделий А и х2 изделий Б.

Z=( 12-( 7+ 0,2 х1)) х1+( 10-( 8+ 0,2 х2)) х2 →max,

dth=14 height=40 src="images/referats/1508/image130.gif">при ограничениях 13 х1+ 6 х2≤ 90,

8 х1+ 11 х2≤88,

Преобразуя целевую функцию, получим:

Z=5х1-0,2х+2 х2-0,2х→max

ОДР – многоугольник ОАВD. Для построения линий уровня функции, приведём функцию к следующему виду:

(х1-12,5)2+(х2-5)2=181,25-5Z .

Линиями уровня будут окружности с центром в точке О1(12,5; 5) и радиуса . Окружность наибольшего радиуса будет проходить через точку М, находящейся на пересечении прямой ВD и прямой O1М, перпендикулярной к BD. Найдём координаты точки М.

13х1+ 6х2=90

х2-5=6/13(х1-12,5). Решив систему, получим, М(6;2).

Z(М)=30-7,2-2,8+4=26.

Ответ: Для получения предприятием максимальной прибыли, составляющей 26 ден.ед., следует выпустить 6 ед. изделия А и 2 ед. изделия Б.

5) Задача на условный экстремум.

Если система ограничений (3.1) задана в виде равенств, то это задача на условный экстремум. В случае функции n независимых переменных (x1,x2, …,хn) задача на условный экстремум формулируется следующим образом:

L=f(x1,x2, …,хn )→max (min)

при условиях: gi(x1,x2, …,хn)=0, i=. (m<n).

В конце XVIII века Лагранж предложил остроумный метод решения задачи на условный экстремум. Суть метода Лагранжа состоит в построении функции L(x1,x2, …,хn)= f(x1,x2, …,хn)+gi(x1,x2, …,хn), где λi неизвестные постоянные, и нахождении экстремума функции L.

Верна следующая теорема: если точка () является точкой условного экстремума функции f(x1,x2, …,хn) при условии g(x1,x2, …,хn)=0, то существует значение λi такие, что точка () является точкой экстремума функции L().

Рассмотрим метод Лагранжа для функции двух переменных.

L(x1,x2,λ)= f(x1,x2)+λ g(x1,x2)

Таким образом, для нахождения условного экстремума функции f(x1,x2) при условии g(x1,x2)=0 требуется найти решение системы

L=f (x1,x2)+λg(x1,x2)=0, (3.18)

L=f (x1, x2) +λg(x1, x2) =0,

L= g(x1, x2) =0. [4]

Есть и достаточные условия, при выполнении которых решение (x1,x2,λ) системы (3.18) определяет точку, в которой функция f достигает экстремума, для этого нужно вычислить значения и составить определитель

=-.

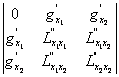Если <0, то функция имеет в точке () условный максимум, если >0 – то условный минимум.

Решим задачу методом множителей Лагранжа.

Общие издержки производства заданы функцией Т=0,5х2+0,6ху+0,4у2+ +700х+600у+2000, где х и у соответственно количество товаров А и В. Общее количество произведённой продукции должно быть равно 500 единиц. Сколько единиц товара А и В нужно производить, чтобы издержки на их изготовление были минимальными?

Решение: составим функцию Лагранжа.

L(x, y, λ) =0,5х2+0,6ху+0,4у2+ +700х+600у+2000+λ(х+у-500). Приравнивая к нулю её частные производные, получим

х+0,6у+700+ λ=0,

0,6х+0,8у+600+ λ=0,

х+у-500=0.

Решив систему, найдём (0, 500, -1000).

Воспользуемся достаточным условием для определения найденного значения L(x0,y0)=1, L(x0,y0)=0.8, L(x0,y0)=0.6. Функция g= х+у-500. g=1, g=1.

=-(0·L·L+ g·L· g+ g·g·L- g·L·g-0·L·L- g· g·L)=0,6>0

Значит, в точке (0;500) функция L имеет условный минимум.

Ответ: Выгодно производить только 500 ед. товара В, а товар А не производить.

Наиболее простым способом нахождения условного экстремума функции двух переменных является сведение задачи к отысканию экстремума функции одной переменной. Пусть уравнение g(x1,x2)=0 удалось разрешить относительно одной из переменных, например, выразить х2 через х1: х2=φ(х1). Подставив полученное выражение в функцию, получим y=f(x1,x2)= y=f(x1, φ(х1)), т.е. функцию одной переменной. Её экстремум и будет условным экстремумом функции y=f(x1,x2).

 Скачать реферат