Векторная алгебра и аналитическая геометрия

.

Расстояние от точки до прямой находится по формуле

.

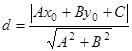Пример 7. Даны уравнения двух сторон прямоугольника eight=21 src="images/referats/11812/image153.png">, и уравнение его диагонали . Составить уравнения

Решение. Сделаем схематический чертеж (Рис.6). Перепишем данные уравнения в виде: , , . Так как угловые коэффициенты прямых, задающих стороны прямоугольника, одинаковы , то эти уравнения задают параллельные прямые, то есть стороны, на них лежащие, противоположны. Найдем точки пересечения данной диагонали с этими сторонами. Пусть это будут точки и . Для этого приравняем сначала 1 и 3, а затем 2 и 3 уравнения:

; . Таким образом, .

Неизвестные стороны параллельны между собой и перпендикулярны данным (так как это прямоугольник).

Замечание. Угловые коэффициенты перпендикулярных прямых и связаны соотношением .

Таким образом, уравнения неизвестных сторон прямоугольника таковы:

. Подставив в первое уравнение координаты точки , во второе – точки , получим, что и, следовательно, , .

Найдем координаты точек и , приравняв уравнения соответствующих сторон:

, то есть ;

, то есть .

Уравнение диагонали получим как уравнение прямой, проходящей через две заданные точки и :

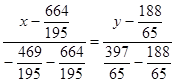или .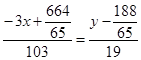

Уравнения прямой в пространстве. Прямая в пространстве Oxyz определяется как линия пересечения двух плоскостей 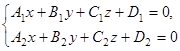(общие уравнения прямой в пространстве).

Канонические уравнения прямой в пространстве имеют вид

,

где – точка, через которую проходит прямая, а вектор , параллельный данной прямой, называется направляющим вектором прямой.

Уравнения прямой в пространстве, проходящей через две заданные точки и имеют вид

.

Угол между двумя прямыми с направляющими векторами и определяется по формуле

.

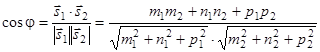Пример 8. Пирамида задана координатами своих вершин , , . Требуется найти:

1) длины ребер и ; 2) угол между ребрами и ; 3) площадь грани, содержащей вершины ; 4) объем пирамиды; 5) уравнения прямых и ;

6) уравнение высоты , опущенной из вершины на плоскость ;

7) расстояние от вершины до плоскости ; 8) угол между ребром и гранью, содержащей вершины .

Решение.1) Длины ребер и определим как модуль векторов и по формулам ;

;

 Скачать реферат