Геометрия места точек на плоскости

Рис. 2

Рис. 3

Выпуклый многоугольник называют правильным, если у него все стороны равны, и все углы равны.

Многоугольник называется вписанным в окружность, если все его вершины лежат на некоторой окружности. Многоугольник называется описанны

м около окружности, если все его стороны касаются некоторой окружности.

Геометрия часто применяется на практике. Её надо знать и рабочему, и инженеру, и архитектору, и художнику. Одним словом, геометрию надо знать всем.

Планиметрия – это раздел геометрии, в котором изучаются фигуры на плоскости.

Фигура – это произвольное множество точек на плоскости. Точка, прямая, отрезок, луч, треугольник, круг, квадрат и так далее – всё это примеры геометрических фигур.

Основными геометрическими фигурами на плоскости являются точка и прямая. Этим фигурам в геометрии не даётся определений.

Также не определяются такие понятия (отношения), как «лежать между», «принадлежать», «проходить через…» и так далее.

Остальным геометрическим фигурам и другим понятиям даются определения. Определение – это предложение, в котором разъясняется смысл и содержание того или иного понятия. При этом разъяснение состоит в том, что оно сводится к ранее определённым понятиям.

Существует несколько подходов к построению курса планиметрии (и геометрии в целом): аксиоматический, аналитический, векторный, групповой.

Аксиоматическая теория строится следующим образом:

1) даются неопределяемые понятия (в нашем случае это точка и прямая);

2) вводятся неопределяемые отношения (связи между понятиями – «лежать между», «принадлежать» и так далее);

3) даётся система аксиом – то есть утверждений, принимаемых без доказательства;

4) на основе аксиом и законов математической логики доказываются теоремы.

Аксиом, как правило, немного, а вот теорем – бесконечное множество. К аксиомам планиметрии можно отнести следующие:

1. Какова бы ни была прямая, существуют точки, принадлежащие этой прямой, и точки, не принадлежащие ей.

Через любые две точки можно провести прямую, и только одну.

2. Из трёх точек на данной прямой одна и только одна лежит между двумя другими.

3. Каждый отрезок имеет определённую длину, большую нуля. Длина отрезка равна сумме длин его частей, на которые он разбивается любой его точкой.

4. Прямая разбивает плоскость на две полуплоскости.

5. Каждый угол имеет определённую градусную меру, большую нуля. Развёрнутый угол равен 180°. Градусная мера угла равна сумме градусных мер углов, на которые он разбивается любым лучом, проходящим между его сторонами.

6. На любом луче от его начальной точки можно отложить отрезок заданной длины, и только один.

7. От любого луча в заданную полуплоскость можно отложить угол с заданной градусной мерой, меньшей 180°, и только один.

8. Каков бы ни был треугольник, существует равный ему треугольник в заданном расположении относительно данного луча.

9. Через точку, не лежащую на данной прямой, можно провести не более одной прямой, параллельной данной.

3. Основные геометрические места точек на плоскости

Геометрическим местом точек плоскости, равноудалённых от сторон угла, будет биссектриса данного угла (рис. 4). АК = AT, где А – любая точка на биссектрисе.

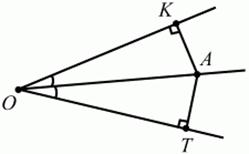
Рис. 4.

Геометрическим местом точек, равноудалённых от двух данных точек, будет прямая, перпендикулярная к отрезку, соединяющему эти точки, и проходящая через его середину (рис. 5). MA = MB, где М – произвольная точка на серединном перпендикуляре отрезка АВ.

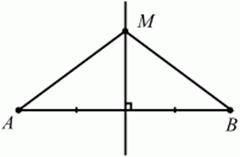
Рис. 5.

Геометрическим местом точек плоскости, равноудалённых от заданной точки, будет окружность с центром в этой точке (рис. 6). Точка О равноудалена от точек окружности.

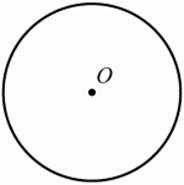
Рис. 6.

Местоположение центра окружности, описанной около треугольника.

Центр окружности, описанной около треугольника, является точкой пересечения перпендикуляров к сторонам треугольника, проведённых через середины этих сторон (рис. 7). А, В, С – вершины треугольника, лежащие на окружности.

АМ = МВ и АК = КС.

Точки М и К – основания перпендикуляров к сторонам АВ и АС соответственно.

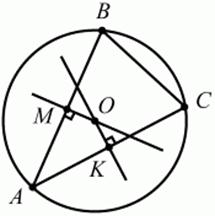
Рис. 7.

Местоположение центра окружности, вписанной в треугольник.

Центр окружности, вписанной в треугольник, является точкой пересечения его биссектрис (рис. 8). В ⊿ABC отрезки AT и СК являются биссектрисами.

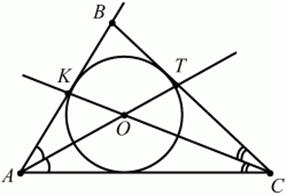
Рис. 8.

4. Примеры задач на геометрические места точек

1. Два колеса радиусов r1 и r2 катаются по прямой l. Найдите множество точек пересечения M их общих внутренних касательных.

Решение :Пусть O1 и O2 — центры колес радиусов r1 и r2 соответственно. Если M — точка пересечения внутренних касательных, то O1M: O2M = r1: r2. Из этого условия легко получить, что расстояние от точки M до прямой l равно 2r1r2/(r1 + r2). Поэтому все точки пересечения общих внутренних касательных лежат на прямой, параллельной прямой l и отстоящей от нее на расстояние 2r1r2/(r1 + r2).

2. Найдите геометрическое место центров окружностей, проходящих через две данные точки.

Решение: Пусть окружность с центром O проходит через данные точки A и B. Поскольку OA = OB (как радиусы одной окружности), точка O лежит на серединном перпендикуляре к отрезку AB. Обратно, каждая точка O, лежащая на серединном перпендикуляре к AB, равноудалена от точек A и B. Значит, точка O — центр окружности, проходящей через точки A и B.

3. Стороны AB и CD четырехугольника ABCD площади S не параллельны. Найдите ГМТ X, лежащих внутри четырехугольника, для которых SABX + SCDX = S/2.

Решение: Пусть O — точка пересечения прямых AB и CD. Отложим на лучах OA и OD отрезки OK и OL, равные AB и CD соответственно. Тогда SABX + SCDX = SKOX + SLOX±SKXL. Следовательно, площадь треугольника KXL постоянна, т. е. точка X лежит на прямой, параллельной KL.

4. На плоскости даны точки A и B. Найдите ГМТ M, для которых разность квадратов длин отрезков AM и BM постоянна.

Решение: Введем систему координат, выбрав точку A в качестве начала координат и направив ось Ox по лучу AB. Пусть точка M имеет координаты (x, y). Тогда AM2 = x2 + y2 и BM2 = (x - a)2 + y2, где a = AB. Поэтому AM2 - BM2 = 2ax - a2. Эта величина равна k для точек M с координатами ((a2 + k)/2a, y); все такие точки лежат на прямой, перпендикулярной AB.

5. Дан прямоугольник ABCD. Найдите ГМТ X, для которых AX + BX = CX + DX.

Решение: Пусть l — прямая, проходящая через середины сторон BC и AD. Предположим, что точка X не лежит на прямой l, например что точки A и X лежат по одну сторону от прямой l. Тогда AX < DX и BX < CX, а значит, AX + BX < CX + DX. Поэтому прямая l — искомое ГМТ.

 Скачать реферат