Типовой расчет

При имеем:

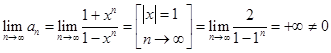
то есть ряд расходится.

Окончательно, получаем ряд расходится при любом Х

Ответ:

9. Найти область сходи

мости функционального ряда

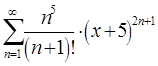
Решение.

Воспользуемся признаком Даламбера:

.

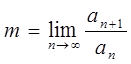В данном примере:

,

.

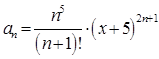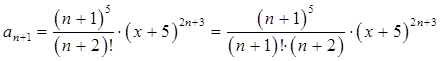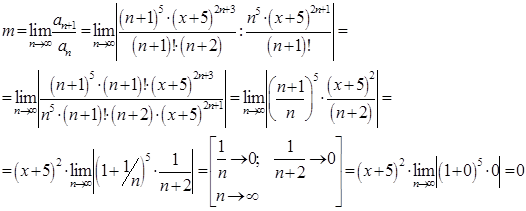
Следовательно, ряд 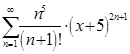сходится при любом Х, т.е.

Ответ: .

10. Найти сумму ряда:

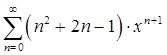
Решение.

Найдём область абсолютной сходимости ряда, пользуясь признаком Даламбера:

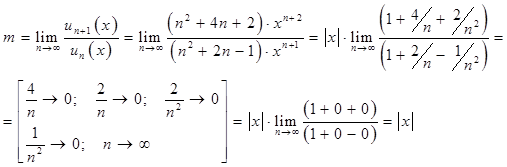
то есть . Ряд сходится для тех значений Х, для которых , то есть , .

При ряд расходится, так как .

Следовательно, .

Перепишем данный ряд:

Обозначим сумму трёх рядов через , и соответственно, тогда

.

Определяем область сходимости этих рядов, пользуясь признаком Даламбера:

1) :

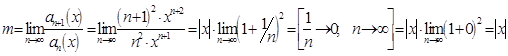
то есть . Ряд сходится для тех значений Х, для которых , то есть , .

Следовательно, .

2) :

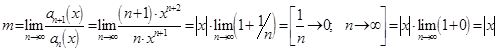
то есть . Ряд сходится для тех значений Х, для которых , то есть , .

Следовательно, .

3) :

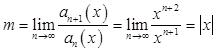
то есть . Ряд сходится для тех значений Х, для которых , то есть , .

Следовательно, .

Найдём сумму ряда .

Это сумма бесконечной геометрической прогрессии: , тогда:

.

Найдём сумму ряда .

.

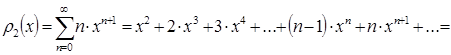
Обозначим сумму ряда в скобках за и проинтегрируем:

.

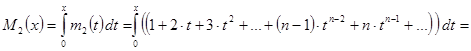
Продифференцируем :

.

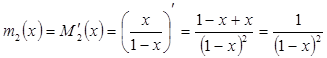Отсюда:

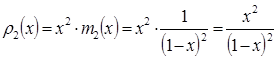
сумму ряда .

.

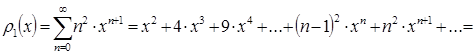
Обозначим сумму ряд в скобках за и проинтегрируем:

.

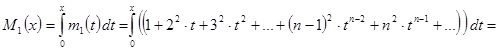
Тогда, продифференцируем :

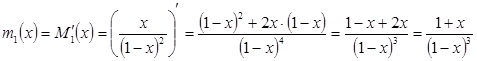
Отсюда:

.

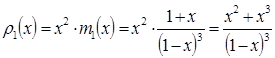Следовательно:

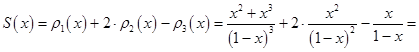
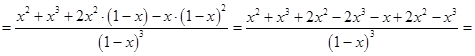
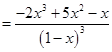для всех .

Ответ:  Скачать реферат