Математизация науки и ее возможности

Удивительно то, что эта простая модель, прекрасно описывающая работу современных компьютеров, родилась раньше, чем появились первые ЭВМ.

Из каких этапов состоит построение математической модели? Это зависит, вообще говоря, от области, в которой разрабатывается эта модель. Например, в экономике этапы можно выделить такие [3]:

1. Определение цели, то есть чего хотят добиться, решая постав

ленную задачу.

2. Определение параметров модели, то есть заранее известных фиксированных факторов, на значение которых исследователь не влияет.

3. Формирование управляющих переменных, изменяя значение которых можно приближаться к поставленной цели. Значения управляющих переменных являются решениями задачи.

4. Определение области допустимых решений, то есть тех ограничений, которым должны удовлетворять управляющие переменные.

5. Выявление неизвестных факторов, то есть величин, которые могут изменяться случайным или неопределенным образом.

6. Выражение цели через управляющие переменные, параметры и неизвестные факторы, то есть формирование целевой функции, называемой также критерием оптимальности задачи.

Это связано со спецификой области: в экономике важны именно такие числовые модели, так как предметная область там в основном состоит из понятий, которые имеют количественный характер. Такие примеры, как машина Тьюринга под эту схему не подходят.

Итак, основные черты метода математического моделирования заключатся в следующем:

· абстракция, некоторое упрощение предметной области, выделение только существенных для исследователя черт рассматриваемого явления

· выявление нужных параметров или характеристик процесса, которые и составляют предмет дальнейшего исследования

· выявление существенных взаимоотношений между этими параметрами

· поиск нужного математического объекта, который будет описывать все исследуемые параметры и отношения между ними

· применение математического аппарата к этому объекту для описания исходного явления

Выражаясь математическим языком, можно сказать, что происходит отображение предметной области, реального явления в математические множества (понятия, структуры). Причем это отображение обладает свойством сохранять некоторые отношения между реальными объектами, в том смысле, что при изменении в реальности происходит похожее изменение и в математическом ее образе.

Не следует думать, что математика всегда располагает необходимым аппаратом для исследования математической модели. Зачастую приходилось открывать новые понятия и методы в математике или разрабатывать старые, чтобы делать это. Например, Ньютон открыл основные понятия дифференциального исчисления, чтобы как раз использовать их в механике. И вообще большинство областей современной математики имеют такое практическое происхождение.

Очень интересен также следующий вопрос: почему же математические модели, сам математический язык настолько полезен для изучения многих явлений в различных науках? Я считаю, что это отчасти связано с непревзойденной строгостью и точностью математического языка, отчасти с его эффективностью и сжатостью. Профессор А.К.Гуц в [4] иллюстрировал эту эффективность следующим отличием гуманитарного мышления от математического. Когда гуманитарий решает какую-нибудь проблему, на пути к ее решению он должен пройти очень большое число промежуточных этапов, на каждом из которых делаются, анализируются и проверяются какие-то логические выводы. Это можно изобразить на диаграмме:

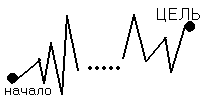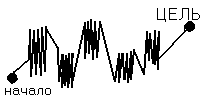здесь “сгустки” – это факты, проверенные другими. Поэтому за тот же промежуток времени математик может сделать гораздо больше.

Адекватность математики при отражении реальности в своих моделях связана с тем, что сама математика, ее понятия и структуры являются не чем иным, как абстракцией самой объективной реальности. Когда мы создаем какое-то множество математических понятий, абстрагируясь от реальных объектов, мы неявно переносим в понятия и связи между этими объектами, которые затем возникают при построении математических моделей. Например, при выделении понятия “натуральное число” как абстракции свойств реальных объектов быть элементом некоторого набора однородных предметов, которые можно переложить один за другим из одной кучки в другую, мы переносим в абстракцию и некоторые свойства натуральных чисел, такие как упорядоченность чисел. При “моделировании” затем скажем коллектива людей, исследуем численность коллектива x (натуральное число) и обнаруживаем, что при добавлении одного индивида, коллектив увеличивается, но увеличивается при этом на 1 и x – мы неявно перенесли упорядоченность реального объекта “коллектив” на его математическую модель “натуральнозначная переменная”. Выдающийся физик, лауреат Нобелевской премии, Поль Дирак говорил: “При построении физической теории следует не доверять всем физическим концепциям. … Следует доверять математической схеме, даже если она, на первый взгляд, не связана с физикой”.

Можно отдельно выделить метод математизации, который неявно является частью математического моделирования: формализация. Он состоит в том, что все изучаемые объекты реальности и отношения между ними заменяются наборами символов и отношений между ними в некотором искусственном языке. Так, в модели машины Тьюринга все объекты – слова в каком-то алфавите, и рассматриваются правила работы с этими словами. Да и вообще, система удобных обозначений – важная часть любой области математики. Этот искусственный язык должен быть по возможности компактным, недвусмысленным и простым. Это отличает его от естественных человеческих языков, для которых характерна некоторая неоднозначность и неопределенность семантики и синтаксиса. Недаром до сих пор не создано удовлетворительных автоматических систем перевода с одного языка на другой. Поэтому важнейшей частью формализации является правильный перевод предметной области на формальный язык. Как пишет Герман Вейль в [6]: “Мощь науки, как свидетельствует развитие современной техники, опирается на комбинацию априорных знаковых конструкций и систематического опыта в форме планируемых и воспроизводимых экспериментов и соответствующих измерений.” В самой математике процесс формализации начался еще с древнегреческого математика Диофанта, который предложил некоторую еще несовершенную систему алгебраических обозначений. Привычные нам обозначения основных математических объектов вводились постепенно, начиная с Виета, Декарта, Лейбница и заканчивая Эйлером, Лагранжем, Коши. Этот процесс продолжается до сих пор, так как каждый день возникают новые и новые математические понятия и объекты.

 Скачать реферат